
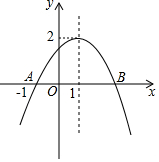
 二次函数y=ax2+bx+c(a≠0)的图如图所示根据图答下列问题:
二次函数y=ax2+bx+c(a≠0)的图如图所示根据图答下列问题:分析 (1)根据抛物线的对称性写出点B的坐标;
(2)方程ax2+bx+c=0的两个根就是抛物线与x轴的两个交点横坐标;
(3)不等式ax2+bx+c<0的解集为抛物线位于x轴下方的部分;
(4)需要根据抛物线的对称轴及开口方向,判断函数的增减性;
(5)可以转化为y=k-1与抛物线y=ax2+bx+c(a≠0)有2个不同的交点.
解答  解:(1)如图所示,A(-1,0),对称轴是x=1,
解:(1)如图所示,A(-1,0),对称轴是x=1,
则点A与B关于x=1对称,
所以B(3,0);
故答案是:(3,0);
(2)如图所示,抛物线与x轴的交点坐标分别是:A(-1,0),B(3,0),
所以方程ax2+bx+c=0的两个根为x1=-1,x2=3;
故答案是:x1=-1,x2=3;
(3)如图所示,不等式ax2+bx+c<0的解集为x<-1或x>3;
故答案是:x<-1或x>3;
(4)如图所示,y随x的增大而减小的自变量x的取值范围为x>1.
故答案是:x>1;
(5)令y=k-1,
方程ax2+bx+c=k-1有两个不相等的实数根时,则y=k-1与抛物线y=ax2+bx+c(a≠0)有2个不同的交点,
所以k-1<2,
解得k<3.
故答案是:k<3.
点评 本题考查了抛物线与x轴的交点和二次函数与不等式.解题时,体现了“数形结合”的数学思想.


科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 8或10 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
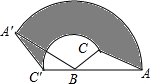 如图,在△ABC中,AB=12cm,BC=6cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的C′处,那么AC边扫过的图形(图中阴影部分)的面积是( )cm2.(结果保留π)
如图,在△ABC中,AB=12cm,BC=6cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的C′处,那么AC边扫过的图形(图中阴影部分)的面积是( )cm2.(结果保留π)| A. | 15π | B. | 60π | C. | 45π | D. | 75π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
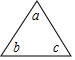 =a+b-c;$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc.
=a+b-c;$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc.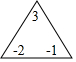
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com