
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE. 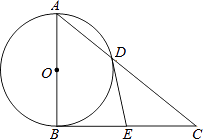
(1)求证:DE与⊙O相切.
(2)若tanC= ![]() ,DE=2,求AD的长.
,DE=2,求AD的长.
【答案】
(1)证明:连接DO,DB,
∴OD=OB,
∴∠ODB=∠OBD.
∵AB是直径,
∴∠ADB=90°,
∴∠CDB=90°.
∵E为BC的中点,
∴DE=BE,
∴∠EDB=∠EBD,
∴∠ODB+∠EDB=∠OBD+∠EBD,
即∠EDO=∠EBO.
∵∠ABC=90°,
∴∠EDO=90°.
∴OD⊥ED于点D.
又∵OD是半径,
∴DE为⊙O的切线
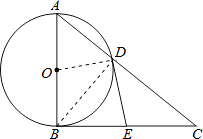
(2)解:∵∠BDC=90°,点E为BC的中点,
∴DE= ![]() BC.
BC.
∵DE=2,
∴BC=4.
在直角△ABC中,tanC= ![]() ,
,
∴AB=BC× ![]() =2
=2 ![]() .
.
在直角△ABC中,由勾股定理得到AC=6.
又∵△ABD∽△ACB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AD= ![]() .
.
【解析】(1)如图,连接DO、DB.欲证明DE与⊙O相切,只需证得OD⊥DE即可;(2)由“直角三角形斜边上的中线等于斜边的一半”易求DE= ![]() BC=2,则BC=4;然后通过解直角△ABC求得AB=2
BC=2,则BC=4;然后通过解直角△ABC求得AB=2 ![]() 、由勾股定理求得AC=6;最后通过△ABD∽△ACB的对应边成比例求得AD=
、由勾股定理求得AC=6;最后通过△ABD∽△ACB的对应边成比例求得AD= ![]() .
.
【考点精析】关于本题考查的切线的判定定理和相似三角形的判定与性质,需要了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ![]() ,反比例函数y=
,反比例函数y= ![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于 .
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度? 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,若“摸出的球是黑球”为必然事件,求m的值;
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于 ![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,分别以AB、BC、DC为边向外作正方形,它们的面积分别为S1、S2、S3.若S2=48,S3=9,则S1的值为( )
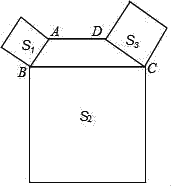
A. 18 B. 12 C. 9 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某无人机于空中A处探测到目标B,D,从无人机A上看目标B,D的俯角分别为30°,60°,此时无人机的飞行高度AC为60m,随后无人机从A处继续飞行30 ![]() m到达A′处,
m到达A′处,
(1)求A,B之间的距离;
(2)求从无人机A′上看目标D的俯角的正切值. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com