
分析 (1)过点P作AD的垂线,交AD于点E,交BC于点F,可证四边形ABFE和CDEF为矩形,则AE=BF,DE=CF,在△PAE,△PCF,△PBF,△PCF中,分别求PA2,PC2,PB2,PD2,再比较PA2+PC2与PB2+PD2即可;
(2)猜想:PA2+PC2=PB2+PD2.
解答 解:(1)过点P作AD的垂线,交AD于点E,交BC于点F,
则四边形ABFE和CDEF为矩形,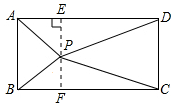
∴AE=BF,DE=CF,
由勾股定理得:
则AP2=AE2+PE2,PC2=PF2+CF2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AE2+PE2+PF2+CF2,
PB2+PD2=BF2+PF2+DE2+PE2,
∴PA2+PC2=PB2+PD2=10,
(2)猜想:PA2+PC2=PB2+PD2.
理由:(1)中已经证明.
点评 本题考查了勾股定理及矩形的性质,解题的关键是学会添加辅助线,构造直角三角形,利用勾股定理解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
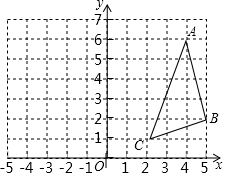 如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A、B的对应点A′、B′的坐标分别是( )
如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A、B的对应点A′、B′的坐标分别是( )| A. | (-3,3)、(-2,4) | B. | (3,-3)、(1,4) | C. | (3,-3)、(-2,4) | D. | (-3,3)、(1,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
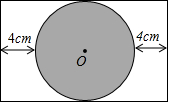 电视显示屏的屏保图是阴影部分的圆O(矩形中最大的圆),屏保图在显示屏(矩形)中的位置如图,若⊙O的面积为400πcm2,求矩形显示屏的长.
电视显示屏的屏保图是阴影部分的圆O(矩形中最大的圆),屏保图在显示屏(矩形)中的位置如图,若⊙O的面积为400πcm2,求矩形显示屏的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 11 | B. | 8 | C. | 7 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x6÷x=x | B. | (x2-$\frac{1}{x}$)÷x=x-1 | C. | x2+x3=x5 | D. | x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com