
| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
分析 设甲商品购进x件,乙商品购进y件,根据“购进甲、乙两种商品共160件、甲商品利润+乙商品利润=1100”列方程组求解可得.
解答 解:设甲商品购进x件,乙商品购进y件,
根据题意,得:$\left\{\begin{array}{l}{x+y=160}\\{5x+10y=1100}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=100}\\{y=60}\end{array}\right.$,
答:甲商品购进100件,乙商品购进60件.
点评 本题主要考查二元一次方程组的应用,理解题意找出题目当中蕴含的等量关系是列方程组求解的关键.


科目:初中数学 来源: 题型:选择题
| A. | 了解全校同学对足球运动的喜欢情况,选男同学进行调查 | |
| B. | 了解某小区居民的防火意识,选6号楼居民进行调查 | |
| C. | 了解商场的平均日营业额,选在周六进行调查 | |
| D. | 了解学生预习新课的情况,选学号是奇数的学生进行调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
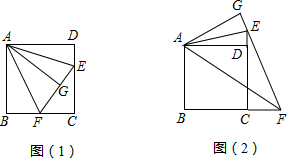
 正方形ABCD和正方形CEFG,连结BF,DF,点P为线段DF的中点,连接GP.
正方形ABCD和正方形CEFG,连结BF,DF,点P为线段DF的中点,连接GP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.则8min时容器内的水量为( )
一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.则8min时容器内的水量为( )| A. | 20 L | B. | 25 L | C. | 27L | D. | 30 L |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com