
| |||||
|
(1)设P1,P4,P8依次为3个班考评分的平均数, W1,W4,W8依次为三个班考评分的中位数, Z1,Z4,Z8依次为三个班考评分的众数. 则:P1= P4= P8= W1=10(分),W4=8(分),W8=9(分), Z1=10(分),Z4=8(分),Z8=9(分) ∴平均数不能反映这三个班的考评结果的差异,而用中位数(或众数)能反映差异,且W1>W8>W4(或Z1>Z8>Z4). (2)给出一种参考答案: 选定行为规范:学习成绩:校运动会:艺术获奖:劳动卫生=3∶2∶3∶1∶1. 设K1、K4、K8依次为3个班的考评分, 则:K1=0.3×10+0.2×10+0.3×6+0.1×10+0.1×7=8.5(分), K4=0.3×10+0.2×8+0.3×8+0.1×9+0.1×8=8.7(分), K8=0.3×9+0.2×10+0.3×9+0.1×6+0.1×9=8.9(分). ∵K8>K4>K1, ∴推荐八(8)班作为市级先进班集体的候选班. |


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源:浙教版(2014) 八年级下 题型:
| |||||
查看答案和解析>>
科目:初中数学 来源:浙教版(2014) 八年级下 题型:
| |||||
查看答案和解析>>
科目:初中数学 来源:人教版(新课标) 九年级(下) 题型:
| |||||
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
小明、小华在一栋电梯楼前感慨楼房真高.小明说:“这楼起码20层!”小华却不以为然:“20层?我看没有,数数就知道了!”小明说:“有本事,你不用数也能明白!”小华想了想说:“没问题!让我们来量一量吧!”小明、小华在楼体两侧各选A、B两点,测量数据如图,其中矩形CDEF表示楼体,AB=150米,CD=10米,∠A=30°,∠B=45°,(A、C、D、B四点在同一直线上)问:
(1)楼高多少米?
(2)若每层楼按3米计算,你支持小明还是小华的观点呢?请说明理由.(参考数据: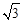 ≈1.73,
≈1.73, ≈1.41,
≈1.41, ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
(1)四边形ABEC一定是什么四边形?
(2)证明你在(1)中所得出的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com