
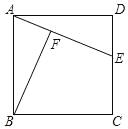
【题目】如图,已知E是正方形ABCD的边CD上一点,BF⊥AE于F.
(1)求证:△ABF∽△EAD;
(2)当AD=2![]() ,
,![]() =
=![]() 时,求AF的长.
时,求AF的长.
【答案】(1)证明见解析;(2)![]() ;
;
【解析】
(1)由正方形的性质,结合BF⊥AE可求得∠ABF=∠DAE,则可证得结论;
(2)利用正方形的性质,结合已知条件可求得DE的长,利用勾股定理可求得AE的长,再利用相似三角形的性质可求得AF的长.
(1)证明:
∵四边形ABCD为正方形,
∴∠DAB=∠D=90°,
∵BF⊥AE,
∴∠AFB=∠D=90°,
∴∠ABF+∠BAF=∠BAF+∠DAE=90°,
∴∠ABF=∠DAE,
∴△ABF∽△EAD;
(2)解:
∵四边形ABCD为正方形,
∴AD=BC=AB=2![]() ,
,
∵![]() =
=![]() ,
,
∴![]() =
=![]() ,解得DE=
,解得DE=![]() ,
,
在Rt△ADE中,由勾股定理可得AE=![]() =
=![]() =5
=5![]() ,
,
∵△ABF∽△EAD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AF=2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知,![]() 是
是![]() 内的一点.
内的一点.
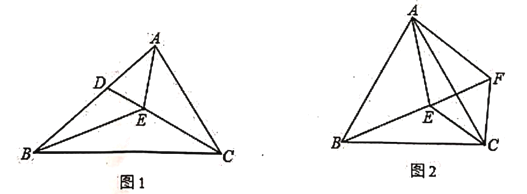
(1)如图,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在线段
在线段![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),且
重合),且![]() ,求证:
,求证:![]() .
.
(2)如图,若![]() 是等边三角形,
是等边三角形,![]() ,
,![]() ,以
,以![]() 为边作等边
为边作等边![]() ,连
,连![]() .当
.当![]() 是等腰三角形时,试求出
是等腰三角形时,试求出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是⊙O的直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④APAD=CQCB.其中正确的是( )
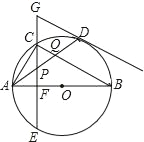
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用3000元购进某种干果销售,由于销售状况良好,很快售完.超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果的数量是第一次的2倍还多300千克,如果超市此时按每千克9元的价格出售,当大部分干果售出后,余下的100千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市第二次销售该种干果盈利了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有下列5个结论,①abc<0; ②2a+b=0;③b2﹣4ac<0;④a+b+c>0;⑤a﹣b+c<0.其中正确的结论有________(填序号)
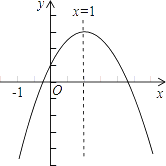
查看答案和解析>>
科目:初中数学 来源: 题型:
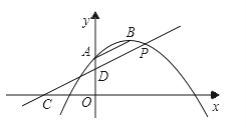
【题目】已知抛物线y=ax2﹣4ax+c经过点A(0,2),顶点B的纵坐标为3.将直线AB向下平移,与x轴、y轴分别交于点C、D,与抛物线的一个交点为P,若D是线段CP的中点,则点P的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣1 | ﹣ | ﹣2 | ﹣ | … |
根据表格中的信息,完成下列各题:
(1)当x=3时,y=________;
(2)当x=_____时,y有最________值为________;
(3)若点A(x1,y1)、B(x2,y2)是该二次函数图象上的两点,且﹣1<x1<0,1<x2<2,试比较两函数值的大小:y1________y2 ;
(4)若自变量x的取值范围是0≤x≤5,则函数值y的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C
处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求隧道AB的长
(![]() ≈1.73).
≈1.73).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com