
����Ŀ����ͼ������A��5��![]() ����������y��ax2+bx�ĶԳ�����x��2����B����������x���һ�����㣬��C��y���ϣ���D�������ߵĶ��㣮
����������y��ax2+bx�ĶԳ�����x��2����B����������x���һ�����㣬��C��y���ϣ���D�������ߵĶ��㣮
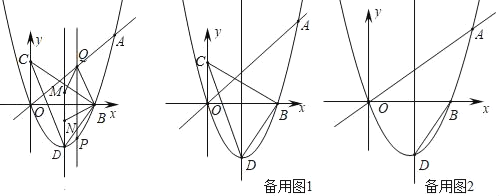
��1����a��b��ֵ��
��2������BCD��ֱ��������ʱ�����OBC�������
��3�����P��ֱ��OA�·�����������y��ax2+bx�ϣ���M��N�������ߵĶԳ����ϣ���M�ڵ�N���Ϸ�������MN��2������P��y���ƽ���߽�ֱ��OA�ڵ�Q����PQ���ʱ����ֱ��д���ı���BQMN���ܳ���Сʱ��Q��M��N�����꣮
���𰸡���1��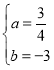 ��2������BDCΪֱ��������ʱ����OBC�������
��2������BDCΪֱ��������ʱ����OBC�������![]() ��
��![]() ����3����Q��M��N������ֱ�Ϊ
����3����Q��M��N������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��
��������
��1���ѵ�A��������뺯������ʽ�����öԳ��᷽�̣����������飬�ⷽ�������a��b��ֵ;
��2�����C�������ǣ�0��m��������û��ָ��ֱ�ǡ�BCD�е�ֱ�ǣ�������Ҫ�������ۣ�����CBD=90�㡢��CDB=90�㡢��BCD=90��ʱ�����ù��ɶ����г�����m�ķ��̣�ͨ���ⷽ�����m��ֵ��Ȼ�����������ε������ʽ���
��3�����ô���ϵ����ȷ��ֱ��OA����ʽΪ![]() �����������ϵ�����������������ľ��빫ʽ��ã�PQ��
�����������ϵ�����������������ľ��빫ʽ��ã�PQ��![]() x(
x(![]() x23x)��
x23x)��![]() x2+
x2+![]() x��
x��![]() (x
(x![]() )2+
)2+![]() ���������ö��κ�����ֵ�������֪����PQ���ʱ���߶�BQΪ����������ΪMN=2������Ҫʹ�ı���BQMN���ܳ���С��ֻ��QM+BN��С��������Գ�-���·������õ���Q��������÷���˼����
���������ö��κ�����ֵ�������֪����PQ���ʱ���߶�BQΪ����������ΪMN=2������Ҫʹ�ı���BQMN���ܳ���С��ֻ��QM+BN��С��������Գ�-���·������õ���Q��������÷���˼����
�⣺��1���߹���A(5�� ![]() )��������y��ax2+bx�ĶԳ�����x��2��
)��������y��ax2+bx�ĶԳ�����x��2��
�� ��
��
��֮����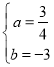 ��
��
��2�����C�������ǣ�0��m�����ɣ�1���ɵ�������![]() ��
��
�������ߵĶ���D�������ǣ�2����3������B�������ǣ�4��0����
����CBD��90��ʱ����BC2+BD2��CD2��
��![]() ��
��
��֮����![]() ��
��
��![]() ��
��
����CDB��90��ʱ����CD2+BD2��BC2��
��![]() ��
��
��֮����![]() ��
��
��![]() ��
��
����BCD��90��ʱ����CD2+BC2��BD2��
��![]() ���˷����⣮
���˷����⣮
��������������BDCΪֱ��������ʱ����OBC�������![]() ��
��![]() ��
��
��3����ֱ��y��kx����A(5�� ![]() )���ɵ�ֱ��
)���ɵ�ֱ��![]() ��
��
�ɣ�1���ɵ�������![]() ��
��
��PQ=![]() x(
x(![]() x23x)��
x23x)��![]() x2+
x2+![]() x��
x��![]() (x
(x![]() )2+
)2+![]() ��
��
�൱x=![]() ʱ��PQ���ʱQ��������
ʱ��PQ���ʱQ��������![]() ��
��
��PQ���ʱ���߶�BQΪ������
��MN��2��
��Ҫʹ�ı���BQMN���ܳ���С��ֻ��QM+BN��С��
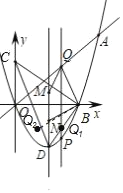
����Q����ƽ��2����λ���ȣ��õ�![]() ������
������![]() ���������ߵĶԳ���ĶԳƵ�
���������ߵĶԳ���ĶԳƵ�![]() ��ֱ��BQ2��Գ���Ľ�����Ƿ��������ĵ�N����ʱ�ı���BQMN���ܳ���С��
��ֱ��BQ2��Գ���Ľ�����Ƿ��������ĵ�N����ʱ�ı���BQMN���ܳ���С��
��ֱ��y��cx+d����![]() �͵�B��4��0����
�͵�B��4��0����
��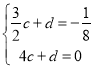 ,
,
��֮����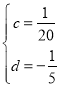 ,
,
��ֱ��![]() ����Q2�͵�B��
����Q2�͵�B��
�ⷽ����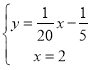 ��
��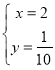 ,
,
���N������Ϊ![]() �����M������Ϊ
�����M������Ϊ![]() ��
��
���Ե�Q��M��N������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������ABC�У���D��E�ֱ��ڱ�AC��AB�ϣ�AG��BC�ڵ�G��AF��DE�ڵ�F����EAF=��GAC��
��1����֤����ADE�ס�ABC��
��2����AD=3��AB=5����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ��ڡ�O��AB��AC����BAC��60����ADΪ��ֱ����BE��AC��AD��P��BE���ӳ��߽���O�ڵ�F������AF��CF��AD��BC��G���ڲ��������������ߵ�����£�ͼ�г�AB��AC�⣬��ȵ��߶ι��У��������ԣ�
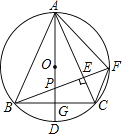
A.2B.3C.4D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��ax2+bx+c��a��0���Գ���Ϊֱ��x����1���䲿��ͼ����ͼ��ʾ�������н��ۣ�
��b2��4ac��0��
��2a��b��
��t��at+b����a��b��tΪ����ʵ������
��3b+2c��0��
�ݵ㣨��![]() ��y1������
��y1������![]() ��y2������
��y2������![]() ��y3���Ǹ��������ϵĵ㣬��y1��y3��y2��
��y3���Ǹ��������ϵĵ㣬��y1��y3��y2��
������ȷ���۵ĸ����ǣ�������
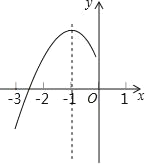
A.5B.4C.3D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
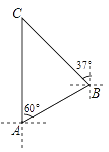
����Ŀ��֪ʶ�ı����磬�Ƽ��ı�����.����װ���IJ��ϸ��¼��������ǵij���.��ͼ��ijУ��֯ѧ���˳�������̲����C��ʾ����չ���ʵ�����������A�غ���C��ǡ����A�ص����������Ҿ���A��13ǧ�ף�������ʾ����Ӧ�ر�ƫ��60��������ʻ��B�أ����ر�ƫ��37��������ʻһ�ξ�����ܵ���C�أ���B��C���صľ���.���ο����ݣ�sin53���![]() ,cos53���
,cos53���![]() ��tan53���
��tan53���![]() )
)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC�У���C��90����AD�ǡ�BAC�Ľ�ƽ���ߣ�
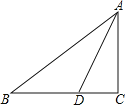
��1����߹���ͼ������O��ʹԲ��O��AB�ϣ���ADΪ��O��һ���ң�����д������������ͼ�ۼ�����
��2���ж�ֱ��BC��������O��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����λ������ǧλ�������λ����֮��Ϊ![]() ��ʮλ�������λ����֮��Ϊ
��ʮλ�������λ����֮��Ϊ![]() �����
�����![]() ����ô�������λ��Ϊ���Գ�����
����ô�������λ��Ϊ���Գ�����
![]() ��С�����Գ�����Ϊ ����λ��
��С�����Գ�����Ϊ ����λ��![]() ��
��![]() ֮��Ϊ�������Գ���������
֮��Ϊ�������Գ���������![]() ��ֵΪ ��
��ֵΪ ��
![]() һ����λ�����Գ�����
һ����λ�����Գ�����![]() �����İ�λ������ǧλ����
�����İ�λ������ǧλ����![]() ��
��![]() ������λ������ʮλ����֮��Ϊ
������λ������ʮλ����֮��Ϊ![]() ����ǧλ����
����ǧλ����![]() ʹ�ò���ʽ��
ʹ�ò���ʽ�� ǡ��
ǡ��![]() �������⣬��������������������Գ�����
�������⣬��������������������Գ�����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
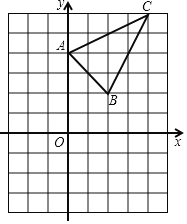
����Ŀ����ͼ����ABC������ƽ���ڣ��������������ֱ�ΪA��0��4����B��2��2����C��4��6���������������У�ÿ��С�����εı߳�Ϊ1��
��1��������ABC����ƽ��5����λ�õ��ġ�A1B1C1����д����B1�����ꣻ
��2���Ե�OΪλ�����ģ��ڵ�����������A2B2C2��ʹ��A2B2C2���ABCλ�ƣ���λ�Ʊ�Ϊ1��2��ֱ��д����C2������͡�A2B2C2�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com