
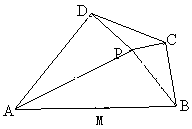
 如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过C,D两点,作边BC,AD的垂线,设两条垂线的交点为P.
如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过C,D两点,作边BC,AD的垂线,设两条垂线的交点为P.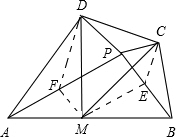 证明:如图:取AP,BP的中点分别为F,E;并连接DF,MF,EC,ME;
证明:如图:取AP,BP的中点分别为F,E;并连接DF,MF,EC,ME; BP=PE,ME=
BP=PE,ME= AP=PF,
AP=PF, PA,CE=BE=PE=
PA,CE=BE=PE= BP,
BP, BP=BE,ME=
BP=BE,ME= AP=DF,进而证明△MDF≌△CME,并根据平行四边形对角相等求证.
AP=DF,进而证明△MDF≌△CME,并根据平行四边形对角相等求证.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
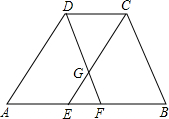 如图,在凸四边形ABCD中,AB∥CD,点E和F在边AB上,且CE∥AD,DF∥BC,DF与CE相交于点G,若△EFG的面积等于1,△CDG的面积等于2,则四边形ABCD的面积等于
如图,在凸四边形ABCD中,AB∥CD,点E和F在边AB上,且CE∥AD,DF∥BC,DF与CE相交于点G,若△EFG的面积等于1,△CDG的面积等于2,则四边形ABCD的面积等于查看答案和解析>>
科目:初中数学 来源: 题型:
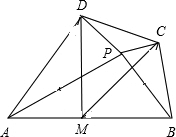 如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过C,D两点,作边BC,AD的垂线,设两条垂线的交点为P.
如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过C,D两点,作边BC,AD的垂线,设两条垂线的交点为P.查看答案和解析>>
科目:初中数学 来源: 题型:
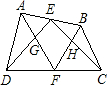 如图,在凸四边形ABCD中,E、F分别为边AB、CD的中点,AF、DE交于点G,BF、CE交于点H,四边形EGFH的面积为10.则△ADG与△BCH的面积和为( )
如图,在凸四边形ABCD中,E、F分别为边AB、CD的中点,AF、DE交于点G,BF、CE交于点H,四边形EGFH的面积为10.则△ADG与△BCH的面积和为( )A、
| ||
| B、10 | ||
| C、15 | ||
| D、20 |
查看答案和解析>>
科目:初中数学 来源:四川省竞赛题 题型:证明题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com