
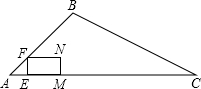
 ��ͼ���ڡ�ABC�У���BAC=45�㣬AB=4$\sqrt{2}$cm��AC=12cm����E�ӵ�A������AC������1cm/s���ٶ��˶�����Cֹͣ����EF��AC������AB-BC�ڵ�F����EFΪ������������EFNM��ʹEM=2EF�����E���˶�ʱ��Ϊt��s����
��ͼ���ڡ�ABC�У���BAC=45�㣬AB=4$\sqrt{2}$cm��AC=12cm����E�ӵ�A������AC������1cm/s���ٶ��˶�����Cֹͣ����EF��AC������AB-BC�ڵ�F����EFΪ������������EFNM��ʹEM=2EF�����E���˶�ʱ��Ϊt��s�������� ��1������������������ۣ��ٵ�E��AO���˶�ʱ����ͼ1���ڵ�E��AO���˶�ʱ����ͼ2���ֱ���ݵ���ֱ�������ε��������EF�ij���
��2������ƽ���߽������γɱ��������б���ʽ�����FN�ij������õ�����ϵʽFN=2EF���е�ʽ��t��ֵ��
��3��������������ۣ��ٵ�0��t��$\frac{12}{5}$ʱ������EFNM��������ABC�ص�����ͼ�ξ��Ǿ��Σ��ڵ�$\frac{12}{5}$��t��4ʱ������EFNM��������ABC�ص�����ͼ��������Σ����=�������-�������������ͼ4���۵�4��t��12ʱ����ͼ2���ص�����ͼ���������Σ�����Ǿ������һ�룻
��4������������������ۣ��ٵ�0��t��$\frac{12}{5}$ʱ����ͼ5���ص�����ͼ��Ϊ����FEA1P���ڵ�$\frac{12}{5}$��t��12ʱ����ͼ6��ͼ7���ص���������������������
��� 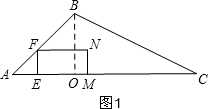 �⣺��1����B��BO��AC��O��
�⣺��1����B��BO��AC��O��
��AB=4$\sqrt{2}$����A=45�㣬
��AO=BO=4��
��E��AO���˶�ʱ����ͼ1����AE=EF=t��
�൱0��t��4ʱ��EF=t��
��E��AO���˶�ʱ����ͼ2����AE=t��EC=12-t��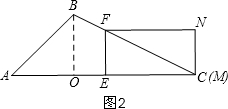
�ߡ�BOC�ס�FEC��
��$\frac{EF}{EC}=\frac{BO}{CO}=\frac{4}{8}$��
��$\frac{EF}{12-t}$=$\frac{1}{2}$��EF=-$\frac{1}{2}$t+6��
�൱4��t��12ʱ��EF=-$\frac{1}{2}$t+6��
�����������ٵ�0��t��4ʱ��EF=t��
�ڵ�4��t��12ʱ��EF=-$\frac{1}{2}$t+6��
��2����ͼ3��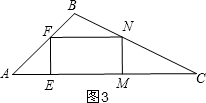 ��N����BC��ʱ��AE=EF=t��
��N����BC��ʱ��AE=EF=t��
��AF=$\sqrt{2}$t��
��BF=4$\sqrt{2}$-$\sqrt{2}$t��
��FN��AC��
��$\frac{FN}{AC}=\frac{BF}{AB}$��
��$\frac{FN}{12}=\frac{4\sqrt{2}-\sqrt{2}t}{4\sqrt{2}}$��
��FN=-3t+12��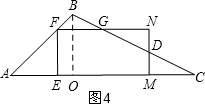
��FN=2EF��
��-3t+12=2t��t=$\frac{12}{5}$��
��N����BC��ʱ��t=$\frac{12}{5}$��
��3���ٵ�0��t��$\frac{12}{5}$ʱ��S=S����EFNM=2t2��
�ڵ�$\frac{12}{5}$��t��4ʱ����ͼ4����FG=-3t+12��FE=t��
��NG=2t-��-3t+12��=5t-12��
��DM��AO��
��$\frac{DM}{AO}=\frac{CM}{CO}$��
��$\frac{DM}{4}=\frac{12-3t}{8}$��
��DM=6-$\frac{3}{2}$t��DN=t-��6-$\frac{3}{2}$t��=$\frac{5}{2}$t-6��
��S=S����FEMN-S��DGN=2t2-$\frac{1}{2}$��5t-12����$\frac{5}{2}$t-6��=$-\frac{17}{4}$t2+30t-36��
�۵�4��t��12ʱ����ͼ2��S=$\frac{1}{2}$S����FEMN=t2��
��4��AA1=2t��CC1=2��12-3t��=24-6t��
�ٵ�0��t��$\frac{12}{5}$ʱ����ͼ5���ص�����ͼ��Ϊ����FEA1P��
��A1E=A1A-AE=2t-t=t��
�ص��������S1=A1E•EF=t2��
�ڵ�$\frac{12}{5}$��t��4ʱ���ص��������S1=��AA1+CC1-12��2=��12-4t��2��
��t=$\frac{13}{4}$��t=$\frac{11}{4}$ʱ��S1=1��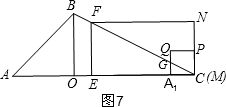
�۵�4��t��12ʱ����ͼ7����C��C1�غϣ��ص����������Ȼ�������Σ�
������������t=1��$\frac{13}{4}$��$\frac{11}{4}$��
���� �������ı��ε��ۺ��⣬�����������ε����ʺ��ж����Լ����ɶ������������й�֪ʶ����������ۺ��Ե���Ŀ����Ҫ�����ո�֪ʶ�������ϵ�ͷ�������˼������ã���Ҫ����ͼ���ص�ѡ����ʵ������ʽ���������������ۺ��Խ�ǿ���ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ��װ��2�������3������ÿ�������ɫ�ⶼ��ͬ���Ĵ�����������һ�����������ʤ�����������һ�ʤ�� | |
| B�� | �ӱ��к���1��100��100�ſ�Ƭ�У������ȡһ�ţ��鵽����Ϊ������ʤ�������һ�ʤ�� | |
| C�� | ������һö�ʵؾ��ȵ����ӣ������ĵ���С��4���ʤ�������ĵ�������4���һ�ʤ�� | |
| D�� | ��С������ͼ��ʾ�ĵذ������ɵع������������ͣ��ij�鷽���ϣ���С��ͣ�ں�ɫ�������ʤ����ͣ�ڰ�ɫ�������һ�ʤ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������OABC�У�AB=1��AO=2��������OABC�Ƶ�O��˳ʱ��ת90�㣬�õ�����OA��B��C����BB��=$\sqrt{10}$��
��ͼ������OABC�У�AB=1��AO=2��������OABC�Ƶ�O��˳ʱ��ת90�㣬�õ�����OA��B��C����BB��=$\sqrt{10}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{\frac{1}{2}}$ | B�� | $\sqrt{0.3}$ | C�� | $\sqrt{8}$ | D�� | $\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��5 | B�� | x��3 | C�� | x��3 | D�� | x��3 �� x��5 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com