
【题目】如图,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点并与
两点并与![]() 轴的另一个交点为
轴的另一个交点为![]() ,且
,且![]() .
.

(1)求抛物线的解析式;
(2)点![]() 为直线
为直线![]() 上方对称轴右侧抛物线上一点,当
上方对称轴右侧抛物线上一点,当![]() 的面积为
的面积为![]() 时,求
时,求![]() 点的坐标;
点的坐标;
(3)在(2)的条件下,连接![]() ,作
,作![]() 轴于
轴于![]() ,连接
,连接![]() 、
、![]() ,点
,点![]() 为线段
为线段![]() 上一点,点
上一点,点![]() 为线段
为线段![]() 上一点,满足
上一点,满足![]() ,过点
,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)![]() ;(2)R(3,3);(3)1或
;(2)R(3,3);(3)1或![]() .
.
【解析】
(1)求出A、B、C的坐标,把A、B的坐标代入抛物线解析式,解方程组即可得出结论;
(2)设R(t,![]() ).作RK⊥y轴于K,RW⊥x轴于W,连接OR.
).作RK⊥y轴于K,RW⊥x轴于W,连接OR.
根据![]() 计算即可;
计算即可;
(3)在RH上截取RM=OA,连接CM、AM,AM交PE于G,作QF⊥OB于H.分两种情况讨论:①点E在F的左边;②点E在F的右边.
(1)当x=0时y=3,
∴C(0,3),
∴OC=3.
∵OC=3OA,
∴OA=1,
∴A(-1,0).
当y=0时x=4,
∴B(4,0).
把A、B坐标代入得![]() 解得:
解得: ,
,
∴抛物线的解析式为![]() .
.
(2)设R(t,![]() ).
).
作RK⊥y轴于K,RW⊥x轴于W,连接OR.

∵![]()
![]()
∵![]() ,
,
∴![]() ,
,![]() (舍去),
(舍去),![]() ,
,
∴R(3,3).
(3)在RH上截取RM=OA,连接CM、AM,AM交PE于G,作QF⊥OB于H.
分两种情况讨论:①当点E在F的左边时,如图1.

∵CR=CO,∠CRM=∠COA,
∴△CRM≌△COA,
∴CM=CA,∠RCM=∠OCA,
∴∠ACM=∠OCR=90°,
∴∠CAM=∠CMA=45°.
∵AC∥PE,
∴∠CAM=∠AGE=45°.
∵∠PEQ=45°,
∴∠AGE=∠PEQ,
∴AM∥EQ,
∴∠MAH=∠QEF.
∵∠QFE=∠MHA=90°,
∴△QEF∽△MAH,
∴![]() .
.
∵OA=1,OH=3,MH=RH-RM=3-1=2,
∴AH=AO+OH=4,
∴EF=2QF.
设CP=m,
∴QH=![]() CP=
CP=![]() m.
m.
∵OC=OH,
∴∠OHC=45°,
∴QF=FH=m,
∴EF=2m,
∴EH=3m.
∵ACPE为平行四边形,
∴AE=CP=m.
∵EH=AH-AE=4-m,
∴3m=4-m,
∴m=1,
∴CP=1.
②当点E在F的右边时,设AM交QE于N.如图2.

∵CR=CO,∠CRM=∠COA,
∴△CRM≌△COA,
∴CM=CA,∠RCM=∠OCA,
∴∠ACM=∠OCR=90°,
∴∠CAM=∠CMA=45°.
∵AC∥PE,
∴∠CAM=∠AGE=45°.
∵∠PEQ=45°,
∴∠AGE=∠PEQ=45°,
∴∠ENG=∠ENA=90°.
∵∠EQF+∠QEF=90°,∠EAN+∠QEF=90°,
∴∠EQF=∠MAB.
∵∠QFE=∠AHM=90°,
∴△QEF∽△AMH,
∴![]() ,
,
∴QF=2EF.
设CP=m,
∴QH=![]() CP=
CP=![]() m.
m.
∵OC=OH,
∴∠OHC=45°,
∴QF=FH=m,
∴EF=![]() m,
m,
∴EH=![]() m.
m.
∵ACPE为平行四边形,
∴AE=CP=m.
∵EH=AH-AE=4-m,
∴4-m=![]() m,
m,
∴m=![]() ,
,
∴CP=![]() .
.
综上所述:CP的值为1或![]() .
.


科目:初中数学 来源: 题型:
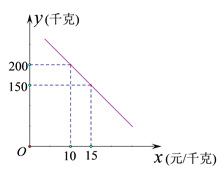
【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为8元/千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间的函数关系如图所示.
(元/千克)之间的函数关系如图所示.
(1)求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“早黑宝”葡萄品种是我省农科院研制的优质新品种,在我省被广泛种植,邓州市某葡萄种植基地2017年种植“早黑宝”100亩,到2019年“卓黑宝”的种植面积达到196亩.
(1)求该基地这两年“早黑宝”种植面积的平均增长率;
(2)市场调查发现,当“早黑宝”的售价为20元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”每天获利1750元,则售价应降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
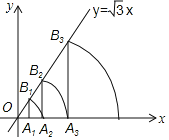
【题目】如图,直线l:y=![]() x,点A1坐标为(1,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1为半径画弧交x轴于点A2;再过点A2作x的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去.
x,点A1坐标为(1,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1为半径画弧交x轴于点A2;再过点A2作x的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去.
求:(1)点B1的坐标和∠A1OB1的度数;
(2)弦A4B3的弦心距的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“阳光体育”活动时间,甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)若已确定甲打第一场,再从其余三位同学中随机选取一位,恰好选中丙同学的概率为 ;
(2)用画树状图或列表的方法,求恰好选中甲、乙两位同学进行比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
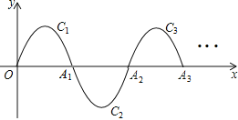
【题目】如图,一段抛物线:![]() 记为
记为![]() ,它与
,它与![]() 轴交于两点
轴交于两点![]() ,
,![]() ;将
;将![]() 绕
绕![]() 旋转
旋转![]() 得到
得到![]() ,交
,交![]() 轴于
轴于![]() ;将
;将![]() 绕
绕![]() 旋转
旋转![]() 得到
得到![]() ,交
,交![]() 轴于
轴于![]() ;…如此进行下去,直至得到
;…如此进行下去,直至得到![]() ,若点
,若点![]() 在第6段抛物线
在第6段抛物线![]() 上,则
上,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西物产丰富,在历史传承与现代科技进步中,特色农林牧业、农产品加工业、传统手工业不断发展革新,富有地域特色和品牌的士特产品愈加丰富.根据市场调查,下面五种特产比较受人们的青睐:![]() 山西汾酒、
山西汾酒、![]() 山西老陈醋、
山西老陈醋、![]() 晋中平遥牛肉、
晋中平遥牛肉、![]() 山西沁州黄小米、
山西沁州黄小米、![]() 运城芮城麻片,某学校老师带领学生在集市上随机调查了部分市民对“我最喜爱的特产”进行投票,将票数进行统计.绘制了如图所示的条形统计图和扇形统计图(均不完整).
运城芮城麻片,某学校老师带领学生在集市上随机调查了部分市民对“我最喜爱的特产”进行投票,将票数进行统计.绘制了如图所示的条形统计图和扇形统计图(均不完整).


请根据图中的信息解答下列问题.
![]() 直接写出参与投票的人数,并补全条形统计图;
直接写出参与投票的人数,并补全条形统计图;
![]() 若该集市上共有
若该集市上共有![]() 人,请估计该集市喜爱运城芮城麻片的人数;
人,请估计该集市喜爱运城芮城麻片的人数;
![]() 若要从这五种特产中随机抽取出两种特产,请用画树状图或列表的方法,求正好抽到山西汾酒和晋中平遥牛肉的概率.
若要从这五种特产中随机抽取出两种特产,请用画树状图或列表的方法,求正好抽到山西汾酒和晋中平遥牛肉的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com