
【题目】(阅读材料)
南京市地铁公司规定:自2019年3月31日起,普通成人持储值卡乘坐地铁出行,每个自然月内,达到规定消费累计金额后的乘次,享受相应的折扣优惠(见图).地铁出行消费累计金额月底清零,次月重新累计.

比如:李老师二月份无储值卡消费260元,若采用新规持储值卡消费,则需付费150×0.95+50×0.9+60×0.8=235.5元.
(解决问题)
甲、乙两个成人二月份无储值卡乘坐地铁消费金额合计300元(甲消费金额超过150元,但不超过200元).若两人采用新规持储值卡消费,则共需付费283.5元.求甲、乙二月份乘坐地铁的消费金额各是多少元?
科目:初中数学 来源: 题型:
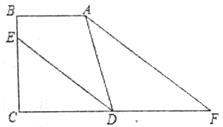
【题目】如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF.求证:∠DAF=∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:
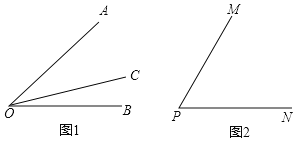
【题目】如图①,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.如图②,若![]() ,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为________.
,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙![]() 与菱形
与菱形![]() 在平面直角坐标系中,点
在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 在点
在点![]() 的右侧.
的右侧.


(![]() )求菱形
)求菱形![]() 的周长.
的周长.
(![]() )若⊙
)若⊙![]() 沿
沿![]() 轴向右以每秒
轴向右以每秒![]() 个单位长度的速度平移,菱形
个单位长度的速度平移,菱形![]() 沿
沿![]() 轴向左以每秒
轴向左以每秒![]() 个单位长度的速度平移,设菱形移动的时间为(
个单位长度的速度平移,设菱形移动的时间为(![]() 秒),当⊙
秒),当⊙![]() 与
与![]() 相切,且切点为
相切,且切点为![]() 的中点时,连接
的中点时,连接![]() ,求
,求![]() 的值及
的值及![]() 的度数.
的度数.
(![]() )在(
)在(![]() )的条件下,当点
)的条件下,当点![]() 与
与![]() 所在的直线的距离为
所在的直线的距离为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣![]() +bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为(﹣2,0).
+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为(﹣2,0).
(1)求抛物线的解析式;
(2)连接AC、BC,求线段BC所在直线的解析式;
(3)在抛物线的对称轴上是否存在点P,使△ACP为等腰三角形?若存在,求出符合条件的P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商人经营甲、乙两种商品,每件甲种商品的利润率为40%,每件乙种商品的利润率为60%,当售出的乙种商品比售出的甲种商品的件数多50%时,这个商人得到的总利润率为50%;那么当售出的甲、乙两种商品的件数相等时,这个商人的总利润率是____.(利润率=利润÷成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com