
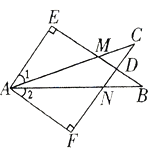
【题目】如图,在△ABE和△ACF中,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF.下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中,正确的是_________.(填序号)
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O交BC于点D,过点D作DE⊥AC,垂足为E. 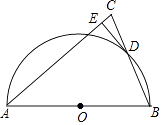
(1)求证:DE是⊙O的切线;
(2)若CE=1,BC=6,求半圆O的半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:已知在△ABC中,边AB上的动点D由A向B运动(与A,B不重合),同时点E由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点,求 ![]() 的值.
的值.
(1)初步尝试
如图(1),若△ABC是等边三角形,DH⊥AC,且点D、E的运动速度相等,小王同学发现可以过点D作DG∥BC交AC于点G,先证GH=AH,再证GF=CF,
从而求得 ![]() 的值为 .
的值为 . 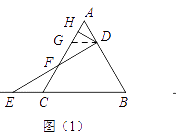
(2)类比探究
如图(2),若△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是 ![]() :1,求
:1,求 ![]() 的值.
的值.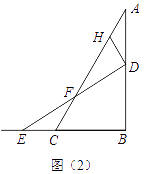
(3)延伸拓展
如图(3)若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记 ![]() =m,且点D、E的运动速度相等,试用含m的代数式表示
=m,且点D、E的运动速度相等,试用含m的代数式表示 ![]() 的值(直接写出果,不必写解答过程).
的值(直接写出果,不必写解答过程).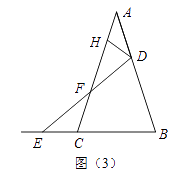
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
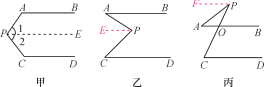
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017 D2017的边长是( ) 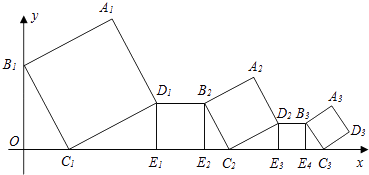
A.( ![]() )2016
)2016
B.( ![]() )2017
)2017
C.( ![]() )2016
)2016
D.( ![]() )2017
)2017
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08) 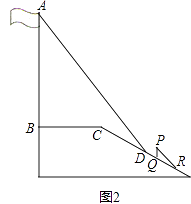
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班长调查了三班近 10 天的数学课堂小测验,在这 10 天,小测验的不及格人数为(单位:个)0,2,0, 3,1,1,0,2,5,1.在这 10 天中小测验不及格的人数( )
A. 中位数为 1.5 B. 方差为 1.5 C. 极差为 1.5 D. 标准差为 1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
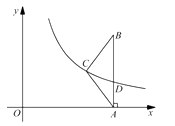
【题目】如图,在 ![]() 中,
中, ![]() ,
, ![]() 轴,垂足为
轴,垂足为 ![]() .反比例函数
.反比例函数 ![]() (
( ![]() )的图像经过点
)的图像经过点 ![]() ,交
,交 ![]() 于点
于点 ![]() .已知
.已知 ![]() ,
, ![]() .
.
(1)若 ![]() ,求
,求 ![]() 的值;
的值;
(2)连接 ![]() ,若
,若 ![]() ,求
,求 ![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com