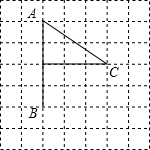练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案，若用（0，-1）表示点B，（0，3）表示A点，那么C点的位置可表示为（　　）
    A．（2，3）B．（1，3）C．（3，1）D．（3，0）

    分析 根据A点的坐标确定坐标系原点位置，然后画出坐标，进而可得答案．

    解答 解：如图所示：C点的位置可表示为（1，3），
    故选：B．

    点评 此题主要考查了坐标确定点的位置，关键是正确确定坐标系原点位置．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    12．若（x+1）0-2（x-2）-2有意义，则x的取值范围是x≠-1且x≠2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

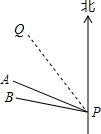    13．如图，台风中心位于点P处，并沿北偏西30°方向PQ移动，已知台风中心移动的速度是30km/h，受台风影响区域的半径为200km．A市位于点P的北偏西60°方向上，与点P的距离为200$\sqrt{3}$km处；B市位于点P的北偏西75°方向上，与点P的距离为210$\sqrt{2}$km处．
    （1）本次台风会影响A市或B市吗？为什么？
    （2）A市或B市若受台风影响，受影响的时间是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．代数基本定理告诉我们对于形如xn+${a}_{1}{x}^{n-1}$$+{a}_{2}{x}^{n-2}$+…+an-1x+an=0（其中a1，a2，…an为整数）这样的方程，如果有整数根的话，那么整数根必定是an的约数．例如方程x3+8x2-11x+2=0的整数根只可能为±1，±2代入检验得x=1时等式成立．故x3+8x2-11x+2含有因式x-1，所以原方程可转化为：（x-1）（x2+9x-2）=0，进而可求得方程的所有解．根据以上阅读材料请你解方程：x3+x2-11x-3=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，在平面直角坐标系中，AC⊥BC于点C，且点C在y的正半轴上，点A和点B分别在x的负半轴和正半轴，AC=BC，AB=8．
    （1）求点C的坐标；
    （2）点D从点C出发以1个单位/秒的速度向y的负半轴方向运动，同时点G从点B出发以1个单位/秒的速度向x轴的正方向运动，连接DG交直线BC于点F．设D、G两点运动时间为t秒，△DOF的面积为s，请用t的式子表示s，并直接写出t的取值范围；
    （3）在（2）的条件下，过点F作FP⊥DF，过点C作x轴的平行线交FP于点P，连接AD，是否存在t，使△CPF的面积等于△AOD面积的2倍？如果存在，请求出t的值；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．利用“等边对等角”
    如图，AB=AD，CD∥AB，CE∥AD．
    求证：△CDE是等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，已知B、D、E、C四点在同一直线上，且AD=AE，∠1=∠2．求证：△ABC是等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图矩形ABCD，A（1，2），矩形ABCD的面积为8，双曲线y=$\frac{k}{x}$正好经过点B，D，两点，且AB∥x轴，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．一透明的敞口正方体容器ABCD-A′B′C′D′装有一些液体，棱AB始终在水平桌面上，容器底部的倾斜角为α（∠CBE=α，如图所示）．

    探究：如图1，液面刚好过棱CD，并与棱BB′交于点Q，此时液体的形状为直三棱柱，其三视图及尺寸如图②．
    解决问题：
    （1）CQ与BE的位置关系是CQ∥BE，BQ的长是3dm，α=37°（注：sin49°=cos41°=$\frac{3}{4}$，tan37°=$\frac{3}{4}$）
    （2）求液体的体积；（参考算法：直棱柱体积V液=底面积SBCQ×高AB）
    （3）在图1的基础上，以棱AB为轴将容器向左或向右旋转，但不能使液体溢出．图3或图4是其正面示意图，若液面与棱C′C或CB交于点P、点Q始终在棱BB′上，设PC=x，BQ=y，分别就图3和图4求y与x的函数关系式，并写出相应的α的范围．

    查看答案和解析>>

    同步练习册答案