
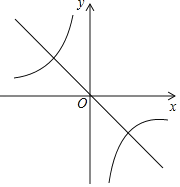
【题目】反比函数![]() 的图象如图所示.
的图象如图所示.
(1)求m的值;
(2)当x>﹣1时,y的取值范围是 ;
(3)当直线y2=﹣x与双曲线![]() 交于A、B两点(A在B的左边)时,结合图象,求出在什么范围时y2>y1?
交于A、B两点(A在B的左边)时,结合图象,求出在什么范围时y2>y1?
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,O为边AC上一点(不与点A,C重合),以OC为半径的圆分别交边BC,AC于点D,E,过点D作DF⊥AB于点F.
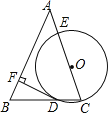
(1)求证:直线DF是⊙O的切线;
(2)若∠A=45°,OC=2,求劣弧![]() 的长.(结果保留π)
的长.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,且
的直径,且![]() ,点
,点![]() 均在
均在![]() 上,
上,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
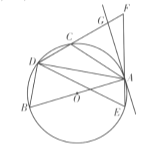
(1)求证:![]() .
.
(2)填空:
①当![]() __________,
__________,![]() 是等腰直角三角形;
是等腰直角三角形;
②当![]() __________,四边形
__________,四边形![]() 是平行四边形.
是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,对角线AC、BD交于点O,E是BC延长线上一点,且AC=EC,连接AE交BD于点P.
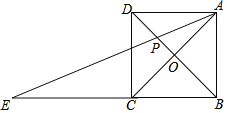
(1)求∠DAE的度数;
(2)求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
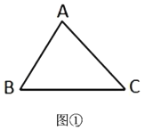
(1)如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 的周长为_________;
的周长为_________;

问题探究
(2)如图②,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,求四边形
,求四边形![]() 的面积;
的面积;
问题解决.
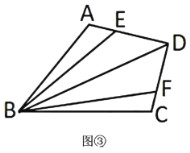
(3)如图③,某农业技术中心为新品种试验而修建了形状为四边形![]() 的试验田,
的试验田,![]() 、
、![]() 、
、![]() 是田间小路,点
是田间小路,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() ,其中道路
,其中道路![]() 的长度为100米,计划在四个三角形区域内种植不同的农作物,为及时了解农作物的生长情况,中心决定在点
的长度为100米,计划在四个三角形区域内种植不同的农作物,为及时了解农作物的生长情况,中心决定在点![]() 、
、![]() 处各架设监控器一台,
处各架设监控器一台,![]() 处的监控器的观察范围为
处的监控器的观察范围为![]() ,
,![]() 处的监控器的观察范围为
处的监控器的观察范围为![]() ,经测量,
,经测量,![]() ,
,![]() ,请探究四边形
,请探究四边形![]() 区域的面积是否存在最小值,若存在,请求出它的最小值;若不存在,请说明理由.
区域的面积是否存在最小值,若存在,请求出它的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个y与x的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.例如:y=![]() +1的图象向左平移2个单位,再向下平移1个单位得到y=
+1的图象向左平移2个单位,再向下平移1个单位得到y=![]() 的图象,则y=
的图象,则y=![]() +1是y与x的“反比例平移函数”.
+1是y与x的“反比例平移函数”.
(1)若(x+3)(y+2)=8,求y与x的函数表达式,并判断这个函数是否为“反比例平移函数”?
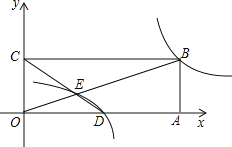
(2)如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A、C的坐标分别为(9,0)、(0,3),点D是OA的中点,连接OB、CD交于点E,“反比例平移函数”y=![]() 的图象经过B、E两点,则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
的图象经过B、E两点,则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
(3)在(2)的条件下,已知过线段BE中点的一条直线l交这个“反比例平移函数”图象于P、Q两点(P在Q的右侧),若B、E、P、Q为顶点组成的四边形面积为16,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
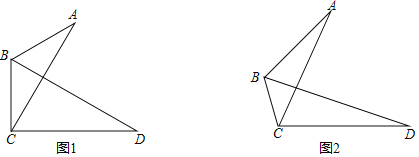
【题目】在△ABC中,∠ABC=120°,线段AC绕点C顺时针旋转60°得到线段CD,连接BD.
(1)如图1,若AB=BC,求证:BD平分∠ABC;
(2)如图2,若AB=2BC,
①求![]() 的值;
的值;
②连接AD,当S△ABC=![]() 时,直接写出四边形ABCD的面积为 .
时,直接写出四边形ABCD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
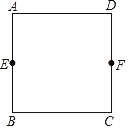
【题目】如图,正方形纸片ABCD边长为6,点E,F分别是AB,CD的中点,点G,H分别在AD,AB上,将纸片沿直线GH对折,当顶点A与线段EF的三等分点重合时,AH的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,一次函数![]() 的图像交x轴于点A,交y轴于点B且与反比例函数
的图像交x轴于点A,交y轴于点B且与反比例函数![]() (k为常数,k≠0)的图象分别交于C、D两点,过点C作
(k为常数,k≠0)的图象分别交于C、D两点,过点C作![]() 轴于M,
轴于M,![]() ,
,![]() ,
,![]()
(1)求直线AB和反比例函数的解析式.
(2)结合图象直接写出:当![]() 时,x的取值范围.
时,x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com