
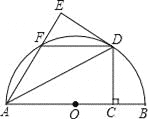
【题目】如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD丄AB交半圆O于点D,将△ACD沿AD折叠得到△AED,AE交半圆于点F,连接DF.
(1)求证:DE是半圆的切线:
(2)连接0D,当OC=BC时,判断四边形ODFA的形状,并证明你的结论.
【答案】(1)证明见解析(2)四边形ODFA是菱形
【解析】试题分析:(1)连接OD,由等腰三角形的性质可得到∠OAD=∠ODA,由图形翻折变换的性质可得到∠CDA=∠EDA,再根据CD⊥AB即可得出结论;
(2)连接OF,可知OC=BC=![]() OB=
OB=![]() OD,由平行线的判定定理可得出OD∥AF,进而可得出△FAO是等边三角形,由等边三角形的性质可判断出四边形ODFA是平行四边形,由OA=OD即可得出结论.
OD,由平行线的判定定理可得出OD∥AF,进而可得出△FAO是等边三角形,由等边三角形的性质可判断出四边形ODFA是平行四边形,由OA=OD即可得出结论.
试题解析:(1)如图,连接OD,则OA=OD,
∴∠OAD=∠ODA,
∵△AED由△ACD对折得到,
∴∠CDA=∠EDA,
又∵CD⊥AB,
∴∠CAD+∠CDA=∠ODA+∠EDA=90°,D点在半圆O上,
∴DE是半圆的切线;
(2)四边形ODFA是菱形,
如图,连接OF,
∵CD⊥OB,
∴△OCD是直角三角形,
∴OC=BC=![]() OB=
OB=![]() OD,
OD,
在Rt△OCD中,∠ODC=30°,
∴∠DOC=60°,
∵∠DOC=∠OAD+∠ODA,
∴∠OAD=∠ODA=∠FAD=30°,
∴OD∥AF,∠FAO=60°,
又∵OF=OA,
∴△FAO是等边三角形,
∴OA=AF,
∴OD=AF,
∴四边形ODFA是平行四边形,
∵OA=OD,
∴四边形ODFA是菱形.



 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠MAN=120°,AC平分∠MAN.B、D分别在射线AN、AM上.
(1)在图1中,当∠ABC=∠ADC=90°时,求证:AD+AB=AC
(2)若把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,如图2所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:由绝对值的意义可知:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .利用这一特性,可以帮助我们解含有绝对值的方程.比如:方程
.利用这一特性,可以帮助我们解含有绝对值的方程.比如:方程![]() ,
,
当![]() 时,原方程可化为
时,原方程可化为![]() ,解得
,解得![]() ;
;
当![]() 时,原方程可化为
时,原方程可化为![]() ,解得
,解得![]() .
.
所以原方程的解是![]() 或
或![]() .
.
(1)请补全题目中横线上的结论.
(2)仿照上面的例题,解方程:![]() .
.
(3)若方程![]() 有解,则
有解,则![]() 应满足的条件是 .
应满足的条件是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
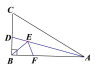
【题目】如图,在Rt△ABC中,AB=6, ∠BAC=30, ∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,则BE+EF的最小值是___
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点![]() 、点
、点![]() 表示的数分别为
表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点表示的数为
的中点表示的数为![]() .
.
(问题情境)
如图,数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为8,点
表示的数为8,点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为![]() 秒(
秒(![]() ).
).
(综合运用)
(1)填空:
①![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ________,线段
________,线段![]() 的中点表示的数为__________.
的中点表示的数为__________.
②用含![]() 的代数式表示:
的代数式表示:![]() 秒后,点
秒后,点![]() 表示的数为____________;点
表示的数为____________;点![]() 表示的数为___________.
表示的数为___________.
③当![]() _________时,
_________时,![]() 、
、![]() 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.
(2)当![]() 为何值时,
为何值时,![]() .
.
(3)若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
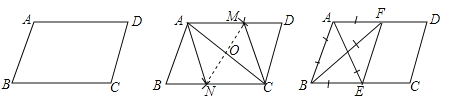
【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.根据两人的作法可判断( )
A. 甲正确,乙错误 B. 乙正确,甲错误
C. 甲、乙均正确 D. 甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
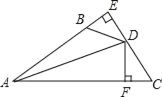
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AC﹣AB=2BE中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瑞瑞有一个小正方体,6个面上分别画有平行四边形、圆、等腰梯形、菱形、等边三角形和直角梯形这6个图形.抛掷这个正方体一次,向上一面的图形既是轴对称图形,又是中心对称图形的概率是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com