
分析 先化简分式,然后根据分式有意义的条件即可求出答案
解答 解:原式=$\frac{{x}^{2}-2x+4+2x-{x}^{2}-2+x}{x-1}$•$\frac{1-x}{{x}^{2}-4}$
=$\frac{x+2}{x-1}$•$\frac{-(x-1)}{(x+2)(x-2)}$
=-$\frac{1}{x-2}$
∵$\left\{\begin{array}{l}{x-1≠0}\\{{x}^{2}-4≠0}\end{array}\right.$
∴x≠1且x≠±2
∴x只能取0,
∴原式=$\frac{1}{2}$
点评 本题考查分式的化简求值,解题的关键是熟练运用分式的运算法则,本题属于基础题型.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
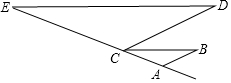 已知:如图,AB∥CD,∠B=∠D,求证:∠E=∠BCA
已知:如图,AB∥CD,∠B=∠D,求证:∠E=∠BCA查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
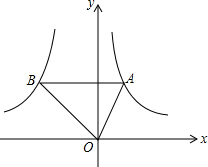 如图,点A是反比例函数y1=$\frac{2}{x}$(x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数y2=$\frac{k}{x}$(k<0,x<0)的图象于点B,且S△AOB=5.
如图,点A是反比例函数y1=$\frac{2}{x}$(x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数y2=$\frac{k}{x}$(k<0,x<0)的图象于点B,且S△AOB=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com