
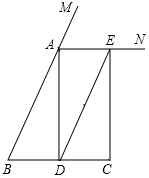
 已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.
已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.  亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
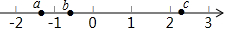 已知实数a,b,c在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-|a+b|+|c+a|+$\sqrt{{(b-c)}^{2}}$-$\root{3}{{c}^{3}}$.
已知实数a,b,c在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-|a+b|+|c+a|+$\sqrt{{(b-c)}^{2}}$-$\root{3}{{c}^{3}}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
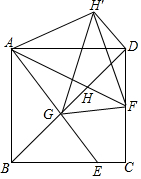 如图,正方形ABCD的边长为4,点E是BC上的一点,连接AE,AF平分∠DAE交DC于点F,连接BD分别交AE,AF于点G,H,将△ADH沿直线AD翻折,点H落在点H′处,连接GH′,H′F,FG,若DF=FC,则△H′GF的面积是4.
如图,正方形ABCD的边长为4,点E是BC上的一点,连接AE,AF平分∠DAE交DC于点F,连接BD分别交AE,AF于点G,H,将△ADH沿直线AD翻折,点H落在点H′处,连接GH′,H′F,FG,若DF=FC,则△H′GF的面积是4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 把所有商品逐渐进行检验 | |
| B. | 从中抽取1件进行检验 | |
| C. | 从中挑选几件进行检验 | |
| D. | 从中按抽样规则抽取一定数量的商品进行检验 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
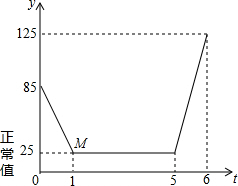 近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.小强家PM2.5的浓度随着时间变化的图象如图所示,请根据图象解答下列问题:
近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.小强家PM2.5的浓度随着时间变化的图象如图所示,请根据图象解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com