
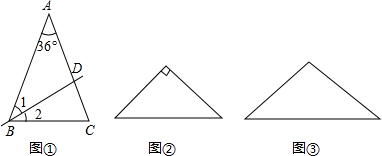
过等腰△ABC一个顶点和它的对边上一点作一条线段,这条线段把原三角形分成两个小的三角形.如果这两个小三角形都是等腰三角形,求△ABC的三个内角的度数.
|
解:设在等腰△ABC中,AB=AC (1)(图1)若D是BC上一点,且AD=BD=CD,则△ABC中,∠B=∠C=
(2)(图2)若D是BC上一点,由于AB=AC>AD,所以当AB=BD,AD=CD时 设∠C=α,则∠B=∠CAD=α,∠BDA=∠BAD=2α 因为∠B+∠BAC+∠C= 则△ABC中,∠B=∠C= (3)(图3)若D是AC上一点,且AD=BD=BC,设∠A=α,则 ∠BDC=∠C=2α,∠ABD=∠DBC=α, 因为∠A+∠ABC+∠C= 则△ABC中,∠A=
(4)(图4)若D是AC上一点,且AD=BD,DC=BC,设∠A=α,则∠ABD=α,∠BDC=∠CBD=2α,∠C=∠ABC=3α, 因为∠A+∠ABC+∠C= 则△ABC中,∠B=∠C= 由等腰三角形的对称性,其他情况(D点在AB上)与(3),(4)相同. |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•长宁区二模)如图,在直角坐标平面中,等腰△ABC的顶点A在第一象限,B(2,0),C(4,0),△ABC的面积是3.
(2012•长宁区二模)如图,在直角坐标平面中,等腰△ABC的顶点A在第一象限,B(2,0),C(4,0),△ABC的面积是3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
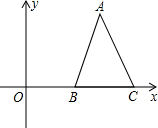 如图,在直角坐标平面中,等腰△ABC的顶点A在第一象限,B(2,0),C(4,0),△ABC的面积是3.
如图,在直角坐标平面中,等腰△ABC的顶点A在第一象限,B(2,0),C(4,0),△ABC的面积是3.查看答案和解析>>
科目:初中数学 来源:2012年四川省广元市虎跳中学中考数学模拟试卷(四)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com