
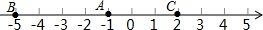 在数轴上有三个点A,B,C,回答下列问题:
在数轴上有三个点A,B,C,回答下列问题: 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
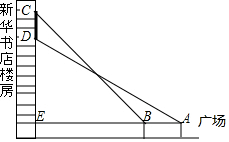 如图,小刚同学在广场上观测新华书店楼房墙上的电子屏幕CD,点A是小刚的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6m到达B处,又测得该屏幕上端C处的仰角为45°,延长AB与楼房垂直相交于点E,测得BE=21m,则该屏幕上端与下端之间的距离CD为(21-9$\sqrt{3}$)m.
如图,小刚同学在广场上观测新华书店楼房墙上的电子屏幕CD,点A是小刚的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6m到达B处,又测得该屏幕上端C处的仰角为45°,延长AB与楼房垂直相交于点E,测得BE=21m,则该屏幕上端与下端之间的距离CD为(21-9$\sqrt{3}$)m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 问题:求解关于x的一元二次不等式a(x-x1)(x-x2)>0(a≠0,x1<x2)
问题:求解关于x的一元二次不等式a(x-x1)(x-x2)>0(a≠0,x1<x2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com