
分析 首先求得这九个数字的立方的位数和,然后将原式变形为(${{x}_{1}}^{3}+{x}_{2}^{3}+{x}_{3}^{3}+…+{x}_{9}^{3}$)-2${x}_{9}^{3}$,从而求得${x}_{9}^{3}$的个位数字是7或2,故此可知${x}_{9}^{3}$是2003或2008,然后再根据所给的不等式即可确定出x9的值.
解答 解:${x}_{1}^{3}+{x}_{2}^{3}+{x}_{3}^{3}+…+{x}_{8}^{3}$=(${{x}_{1}}^{3}+{x}_{2}^{3}+{x}_{3}^{3}+…+{x}_{9}^{3}$)-$2{x}_{9}^{3}$,
∵20013、20023、…20093的个位数字一次是1、8、7、4、5、6、3、2、9,
∴${{x}_{1}}^{3}+{x}_{2}^{3}+{x}_{3}^{3}+…+{x}_{9}^{3}$的个位数字一定是5.
又∵(${{x}_{1}}^{3}+{x}_{2}^{3}+{x}_{3}^{3}+…+{x}_{9}^{3}$)-$2{x}_{9}^{3}$的个位数字是1,
∴${x}_{9}^{3}$的个位数字是7或2,从而${x}_{9}^{3}$是2003或2008.
∵8x9>x1+x2+…+x8,
∴9x9>${{x}_{1}}^{3}+{x}_{2}^{3}+{x}_{3}^{3}+…+{x}_{9}^{3}$.
∴9x9>2005×9.
∴x9>2005.
∴x9=2008.
故答案为:2008.
点评 本题主要考查的是数字的尾数特征,将原式变形为(${{x}_{1}}^{3}+{x}_{2}^{3}+{x}_{3}^{3}+…+{x}_{9}^{3}$)-$2{x}_{9}^{3}$,然后根据尾数特点确定出x9的值是解题的关键.


科目:初中数学 来源: 题型:解答题
 小明和小亮进行百米赛跑,小明比小亮跑得快.如果两人同时起跑,小明肯定赢.现在小明让小亮先跑若干米.途中l1,l2分别表示两人所跑路程与时间的关系.根据图象回答:
小明和小亮进行百米赛跑,小明比小亮跑得快.如果两人同时起跑,小明肯定赢.现在小明让小亮先跑若干米.途中l1,l2分别表示两人所跑路程与时间的关系.根据图象回答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
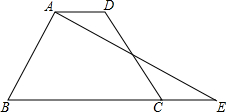 如图,在四边形ABCD中,点F是边CD上一点,连结AF,并延长AF交BC的延长线于点E,使得△ADF与△FCE全等.
如图,在四边形ABCD中,点F是边CD上一点,连结AF,并延长AF交BC的延长线于点E,使得△ADF与△FCE全等.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半釉上,点F在AB上,点B、E在反比例函数$y=\frac{k}{x}$的图象上OA=1,OC=4.
如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半釉上,点F在AB上,点B、E在反比例函数$y=\frac{k}{x}$的图象上OA=1,OC=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com