练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    草原上有4口油井，位于四边形ABCD的四个顶点上，如图所示，如果现在要建一个维修站H，试问H 建在何处，才能使它到4口油井的距离HA+HB+HC+HD为最小，说明理由。

    解：维修站应建在四边形两对角线AC、BD的交点H处，理由如下：取不同于H的F点，根据三角形两边之和大于第三边可得：FD+FB >HD+HB，FC+FA>HC+HA，所以：FD+FB+FC+FA>HD+HB+HC+HA，即HD+HB+HC+HA为最小。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：数学教研室 题型：044

    如图，草原上有4口油井，位于四边形ABCD的4个顶点，现在要建立一个维修站H，试问维修站H建在何处，才能使它到4口油井的距离之和HA+HB+HC+HD为最小，说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源：鼎尖助学系列—同步练习(数学 七年级下册)、与三角形有关的线段 题型：044

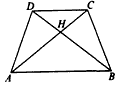
    草原上有4口油井，位于四边形ABCD的4个顶点，如图现在要建一个维修站H，试问H建在何处，才能使它到4口油井的距离HA＋HB＋HC＋HD为最小？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，草原上有4口油井，位于四边形ABCD的4个顶点，现在要建立一个维修站H，试问H建在何处，才能使它到4口油井的距离之和AH+HB+HC+HD为最小，说明理由.

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图10，草原上有4口油井，位于四边形ABCD的4个顶点，现在要建立一个维修站H，试问H建在何处，才能使它到4口油井的距离之和AH+HB+HC+HD为最小，说明理由.

    查看答案和解析>>

    同步练习册答案