
 如果将棱长相等的小正方体按如图的方式摆放,从上到下依次为第一层,第二层,第三层,…,那么第10层的小正方体的个数是55.
如果将棱长相等的小正方体按如图的方式摆放,从上到下依次为第一层,第二层,第三层,…,那么第10层的小正方体的个数是55. 分析 根据图形计算出前几层的正方体的个数,从而得到第n层的个数为1+2+3+…+n,再根据求和公式求出表达式,然后把n=10代入进行计算即可得解.
解答 解:观察不难发现,第一层有1个正方体,
第二层有3个,3=1+2;
第三层有6个,6=1+2+3,
第四层有10个,10=1+2+3+4,
第五层有15个,15=1+2+3+4+5,
…,
第n层有:1+2+3+…+n=$\frac{1}{2}$n(n+1),
当n=10时,$\frac{1}{2}$n(n+1)=$\frac{1}{2}$×10×(10+1)=55.
故答案是:55.
点评 本题是对图形变化规律的考查,仔细观察图形,得到各层的正方体的个数等于连续自然数的和,然后求出第n层的个数的表达式是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
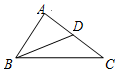 如图,在△ABC中,点D是边AC的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示).
如图,在△ABC中,点D是边AC的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
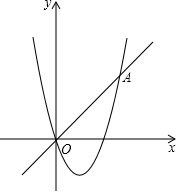 已知,一次函数y=x与二次函数y=x2+bx+c的图象相交于原点O 和点A(4,4)两点.
已知,一次函数y=x与二次函数y=x2+bx+c的图象相交于原点O 和点A(4,4)两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.201×10-4 | B. | 2.01×10-6 | C. | 20.1×10-6 | D. | 2.01×10-5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com