
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
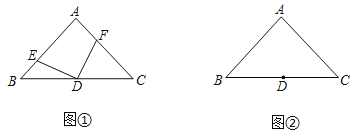
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF.
①求证:BE=AF;
②若S△BDE=![]() S△ABC=2,求S△CDF;
S△ABC=2,求S△CDF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF.
①BE=AF还成立吗?请利用图②说明理由;
②若S△BDE=![]() S△ABC=8,直接写出DF的长.
S△ABC=8,直接写出DF的长.
【答案】(1)①证明见解析;②S△DFC=4;(2)①结论成立.理由见解析;②DF=4![]() .
.
【解析】
(1)①只要证明△BDE≌△ADF(ASA)可得结论.
②求出△ADC,△ADF的面积即可解决问题.
(2)①结论成立,证明方法类似(1).
②利用三角形的面积公式求出AB,再证明AB=2BE,求出DH,EH,利用勾股定理求出DE即可解决问题.
(1)①证明:如图①中,连接AD.
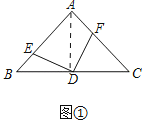
∵AB=AC,∠BAC=90°,BD=DC,
∴AD⊥BC,AD=BD=CD,∠B=∠C=∠DAC=45°,
∵∠EDF=∠BDA=90°,
∴∠BDE=∠ADF,
∴△BDE≌△ADF(ASA),
∴BE=DF.
②解:∵S△BDE=![]() S△ABC=2,
S△ABC=2,
∴S△BDE=2,S△ABC=12,
∵BD=DC,
∴S△ADC=![]() S△ADC=6,
S△ADC=6,
∵△BDE≌△ADF,
∴S△ADF=S△BDE=2,
∴S△DFC=6﹣2=4.
(2)①证明:结论成立.
理由:如图②中,
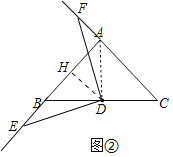
∵AB=AC,∠BAC=90°,BD=DC,
∴AD⊥BC,AD=BD=CD,∠B=∠C=∠DAC=45°,
∵∠EDF=∠BDA=90°,
∴∠BDE=∠ADF,
∴△BDE≌△ADF(ASA),
∴BE=DF.
②解:如图②中,作DH⊥AB于H.
∵S△BDE=![]() S△ABC=8,
S△ABC=8,
∴S△ABC=32,
∴![]() AB2=32,
AB2=32,
∴AB=AC=8,BC=8![]() ,DH=
,DH=![]() AB=4,
AB=4,
∵BD=DC,
∴S△ABD=S△ADC,
∴S△BDE=![]() S△ADB,
S△ADB,
∴AB=2BE,
∴BE=BH=AH=4,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为2、3、4,正放置的四个正方形的面积分别为S1,S2,S3,S4,则S1+S2+S3+S4=______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:OF∥BC;
(2)求证:△AFO≌△CEB;
(3)若EB=5cm,CD=![]() cm,设OE=x,求x值及阴影部分的面积
cm,设OE=x,求x值及阴影部分的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(![]() ,1)在射线OM上,点B(
,1)在射线OM上,点B(![]() ,3)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2017A2018B2018,则点B2018的纵坐标为_______.
,3)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2017A2018B2018,则点B2018的纵坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径
的直径![]() 延长线上的一点,
延长线上的一点,![]() 与
与![]() 相切,切点为
相切,切点为![]() ,点
,点![]() 是
是![]() 上一点,连接
上一点,连接![]() .已知
.已知![]() .下列结论:
.下列结论:
![]() 与
与![]() 相切;
相切;![]() 四边形
四边形![]() 是菱形;
是菱形;![]() ;
;![]() .
.
其中正确的个数为( )

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
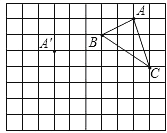
【题目】△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A1,点B1、C1分别是B、C的对应点.
(1)请画出平移后的△A1B1C1(不写画法);
(2)将△A1B1C1绕点C1顺时针旋转90°,画出旋转后的△A2B2C1(不写画法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com