
【题目】甲乙两位同学用围棋子做游戏.如图所示,现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的![]() 个棋子组成轴对称图形,白棋的
个棋子组成轴对称图形,白棋的![]() 个棋子也成轴对称图形.则下列下子方法不正确的是( ),
个棋子也成轴对称图形.则下列下子方法不正确的是( ),![]() .
.

A. 黑(3,7);白(5,3) B. 黑(4,7);白(6,2)
C. 黑(2,7);白(5,3) D. 黑(3,7);白(2,6)
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC,顶点A、B、C都在正方形方格交点上,正方形方格的边长为1.
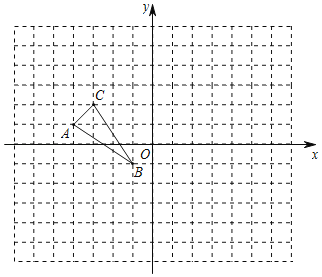
(1)写出A、B、C的坐标;
(2)请在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(3)在y轴上找到一点D,使得CD+BD的值最小,(在图中标出D点位置即可,保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“四书五经”是中国的“圣经”,“四书五经”是《大学》、《中庸》、《论语》和《孟子》(四书)及《诗经》、《尚书》、《易经》、《礼记》、《春秋》(五经)的总称,这是一部被中国人读了几千年的教科书,包含了中国古代的政治理想和治国之道,是我们了解中国古代社会的一把钥匙 . 某学校计划分阶段引导学生读这些书,先购买《论语》和《孟子》供学生阅读 . 已知用500元购买《孟子》的数量和用800元购买《论语》的数量相同,《孟子》的单价比《论语》的单价少15元 . 求《论语》和《孟子》这两种书的单价各是多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.

(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是一座抛物线形拱桥,P 处有一照明灯,水面OA 宽4 m.从O,A 两处观测P 处,仰角分别为α,β,且tanα=![]() ,tanβ=
,tanβ=![]() .以O 为原点,OA 所在直线为x 轴建立平面直角坐标系.
.以O 为原点,OA 所在直线为x 轴建立平面直角坐标系.
(1)求点P的坐标;
(2)若水面上升1 m,则水面宽多少米(![]() 取1.41,结果精确到0.1 m)?
取1.41,结果精确到0.1 m)?

查看答案和解析>>
科目:初中数学 来源: 题型:
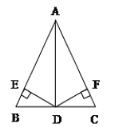
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF.
(1)图中共有_________对全等三角形.
(2)求证:AD是△ABC的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,二次函数
,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,并过点
,并过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .抛物线
.抛物线![]() 和反比例函数
和反比例函数![]() 的图象都经过点
的图象都经过点![]() ,四边形
,四边形![]() 的面积是
的面积是![]() .
.
![]() 求反比例函数、二次函数的解析式及抛物线的对称轴;
求反比例函数、二次函数的解析式及抛物线的对称轴;
![]() 如图
如图![]() ,点
,点![]() 从
从![]() 点出发以每秒
点出发以每秒![]() 个单位的速度沿线段
个单位的速度沿线段![]() 向
向![]() 点运动,点
点运动,点![]() 从
从![]() 点出发以相同的速度沿线段img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/12/08/1a8f9afd/SYS201905120854095644903087_ST/SYS201905120854095644903087_ST.023.png" width="24" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />向
点出发以相同的速度沿线段img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/12/08/1a8f9afd/SYS201905120854095644903087_ST/SYS201905120854095644903087_ST.023.png" width="24" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />向![]() 点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为
点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为![]() 秒.
秒.
①当![]() 为何值时,四边形
为何值时,四边形![]() 为等腰梯形;
为等腰梯形;
②设![]() 与对称轴的交点为
与对称轴的交点为![]() ,过
,过![]() 点作
点作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,设四边形
,设四边形![]() 的面积为
的面积为![]() ,求面积
,求面积![]() 关于时间
关于时间![]() 的函数解析式,并指出
的函数解析式,并指出![]() 的取值范围;当
的取值范围;当![]() 为何值时,
为何值时,![]() 有最大值或最小值.
有最大值或最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,DE垂直平分AB,分别交AB,AC于点E,D.

(1)若∠ADE=40°,求∠DBC的度数;
(2)若BC=6,△CDB的周长为15,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com