
 29、如图,在长方体ABCD-A1B1C1D1中,高AA1=20cm,底面A1B1C1D1是长方形,其长A1B1=10cm,宽A1D1=7cm,点E在B1C1上,且距B1点5cm,一只蚂蚁如果要沿着长方体表面从点A爬到点E,需要爬行的最短路程是多少?
29、如图,在长方体ABCD-A1B1C1D1中,高AA1=20cm,底面A1B1C1D1是长方形,其长A1B1=10cm,宽A1D1=7cm,点E在B1C1上,且距B1点5cm,一只蚂蚁如果要沿着长方体表面从点A爬到点E,需要爬行的最短路程是多少?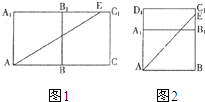 解:将长方体沿B1C1、C1C、CB剪开,向右翻折,使面ABB1A1和面BCC1B1在同一个平面内,连接AE.(如图1)
解:将长方体沿B1C1、C1C、CB剪开,向右翻折,使面ABB1A1和面BCC1B1在同一个平面内,连接AE.(如图1)

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com