
【答案】14![]() 。
。
【考点】轴对称-最短路线问题;勾股定理;垂径定理.
【专题】探究型.
【分析】先由MN=20求出⊙O的半径,再连接OA、OB,由勾股定理得出OD、OC的长,作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,在Rt△AB′E中利用勾股定理即可求出AB′的值.
【解答】∵MN=20,
∴⊙O的半径=10,
连接OA、OB,
在Rt△OBD中,OB=10,BD=6,
∴OD=![]() =
=![]() =8;
=8;
同理,在Rt△AOC中,OA=10,AC=8,
∴OC=![]() =
=![]() =6,
=6,
∴CD=8+6=14,
作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,
在Rt△AB′E中,
∵AE=AC+CE=8+6=14,B′E=CD=14,
∴AB′=![]() =
=![]() =14
=14![]() .
.
故答案为:14![]() .
.
【点评】本题考查的是轴对称-最短路线问题、垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【解题思路】通过读题、审题
(1)完成表格有2个思路:从供或需的角度考虑,均能完成上表。
(2)运用公式(调运水的重量×调运的距离)
总调运量=A的总调运量+B的总调运量调运水的重量×调运的距离
y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275(注:一次函数的最值要得到自变量的取值范围)∵5>0∴y随x的增大而增大,y要最小则x应最大
由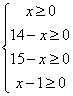 解得1≤x≤14
解得1≤x≤14
y=5x+1275中∵5>0∴y随x的增大而增大,y要最小则x应最小=1
∴调运方案为A往甲调1吨,往乙调13吨;B往甲调14吨,不往乙调。
【答案】⑴(从左至右,从上至下)14-x 15-x x-1
⑵y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275
解不等式1≤x≤14
所以x=1时y取得最小值
y=5+1275=1280
∴调运方案为A往甲调1吨,往乙调13吨;B往甲调14吨,不往乙调。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集在数轴上表示正确的是
A.![]()
![]() B.
B.![]()
![]() C.
C.![]()
![]() D.
D.![]()
![]()
【考点】一次函数与一元一次不等式;在数轴上表示不等式的解集.
【分析】根据图象和交点坐标得出关于x的不等式x+m>kx-1的解集是x>-1,即可得出答案.
【解答】∵直线y1=x+m与y2=kx-1相交于点P(-1,1),
∴根据图象可知:关于x的不等式x+m>kx-1的解集是x>-1,
 在数轴上表示为:
在数轴上表示为:![]()
![]() 。
。
故选B.
查看答案和解析>>
科目:初中数学 来源: 题型:
【答案】1.1×107。
【考点】科学记数法—表示较大的数.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】将11000000用科学记数法表示为:1.1×107.
故答案为:1.1×107.
【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【答案】60°。
【考点】平行线的性质;三角形的外角性质.
【分析】利用三角形的一个外角等于与它不相邻的两个内角的和求出∠3的同位角的度数,再根据两直线平行,同位角相等即可求解.
【解答】如图,∵∠1=130°,∠2=70°,
∴∠4=∠1-∠2=130°-70°=60°,
∵a∥b,
∴∠3=∠4=60°.
故答案为:60°.
【点评】本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,准确识图,理清图中各角度之间的关系是解题的关键.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com