
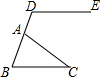
 如图,△ABC中,点D在BA的延长线上,DE∥BC,如果∠BAC=65°,∠C=30°,那么∠BDE的度数是95°.
如图,△ABC中,点D在BA的延长线上,DE∥BC,如果∠BAC=65°,∠C=30°,那么∠BDE的度数是95°. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
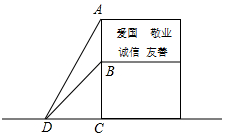 为了弘扬“社会主义核心价值观”,区政府在广场上竖立了如图所示的公益广告牌,并在两侧加固钢缆,已知钢缆底端D到达广告牌立柱AC的距离为5米,从点D测得广告牌顶端A点和底端B点的仰角分别为60°和45°,求广告牌的高度AB.
为了弘扬“社会主义核心价值观”,区政府在广场上竖立了如图所示的公益广告牌,并在两侧加固钢缆,已知钢缆底端D到达广告牌立柱AC的距离为5米,从点D测得广告牌顶端A点和底端B点的仰角分别为60°和45°,求广告牌的高度AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com