
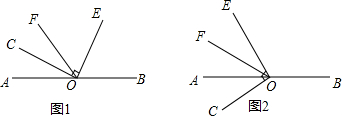
分析 (1)根据互余得到∠EOF=90°-34°,再由OF平分∠AOE,得到∠AOE=2∠EOF=180°-68°,然后根据邻补角的定义得到∠BOE;
(2)当∠COF=n°,根据互余得到∠EOF=90°-n°,再由OF平分∠AOE,得到∠AOE=2∠EOF=180°-2n°,然后根据邻补角的定义得到∠BOE=180°-(180°-2n°)=2n°,所以有∠BOE=2∠COF;
(3)同(2),可得到∠BOE=2∠COF.
解答 解:(1)∵∠COE是直角,∠COF=36°,
∴∠EOF=90°-36°=54°,
∵OF平分∠AOE.
∴∠AOE=2∠EOF=108°,
∴∠BOE=180°-108°=72°;
(2)当∠COF=n°,
∴∠EOF=90°-n°,
∴∠AOE=2∠EOF=180°-2n°,
∴∠BOE=180°-(180°-2n°)=2n°,
∴∠BOE=2∠COF.
故答案为:2n,∠BOE=2∠COF;
(3)∠BOE与∠COF的数量关系仍然成立.理由如下:
设∠COF=n°,
∵∠COE是直角,
∴∠EOF=90°-n°,
又∵OF平分∠AOE.
∴∠AOE=2∠EOF=180°-2n°,
∴∠BOE=180°-(180°-2n°)=2n°,
即∠BOE=2∠COF.
点评 本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等;也考查了角平分线的定义以及互余互补的含义.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
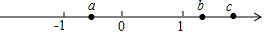 已知实数a,b,c在数轴上的位置如图所示.化简:$\sqrt{{a}^{2}}$+|a+c|-$\sqrt{(a-b)^{2}}$+|1-b|
已知实数a,b,c在数轴上的位置如图所示.化简:$\sqrt{{a}^{2}}$+|a+c|-$\sqrt{(a-b)^{2}}$+|1-b|查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一次函数y=2x+a与y=-x+b的图象都经过A(-2,0),且与y轴分别交于B、C两点.
已知一次函数y=2x+a与y=-x+b的图象都经过A(-2,0),且与y轴分别交于B、C两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
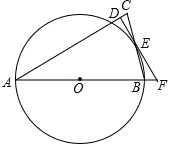 如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作O的切线交AC于点D,且ED⊥AC.
如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作O的切线交AC于点D,且ED⊥AC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
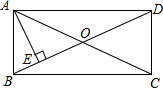 如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$.
如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 七巧板被西方人称为“东方魔板”.下面的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形(如图a)的边长为4,则“一帆风顺”(如图b)阴影部分的面积为1.
七巧板被西方人称为“东方魔板”.下面的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形(如图a)的边长为4,则“一帆风顺”(如图b)阴影部分的面积为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,AB=4$\sqrt{3}$,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
如图,AB是⊙O的直径,AB=4$\sqrt{3}$,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com