

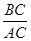 ,求出即可.
,求出即可.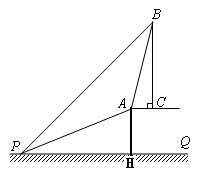
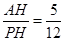 ,
,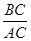 ,
,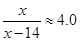 ,
,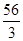 ,即x≈19,
,即x≈19,

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
A.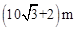 | B.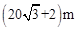 |
C.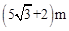 | D.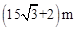 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
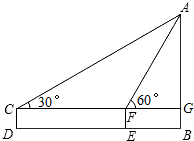
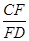 的值为( )
的值为( )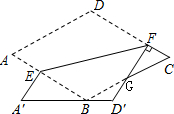
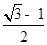
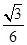 C.
C.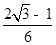
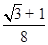
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
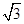 米,加固后大坝的横截面为梯形ABED,CE的长为8米.
米,加固后大坝的横截面为梯形ABED,CE的长为8米.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
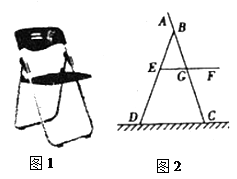
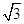 (即AB:BC=1:
(即AB:BC=1: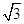 ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).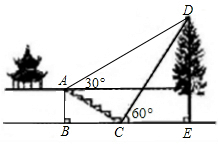
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com