
分析 (1)根据等式中数字的变化,找出猜想;
(2)利用完全平方公式以及通分,可将等式左右两边变形为$\frac{{n}^{2}+2n+1}{n}$,由此即可得出等式成立,即猜想成立.
解答 解:(1)∵2=1+1,3=2+1,4=3+1,…,
∴猜想第n个等式为:(n+1)×$\frac{n+1}{n}$=n+1+$\frac{n+1}{n}$.
(2)证明:左边=(n+1)×$\frac{n+1}{n}$=$\frac{(n+1)^{2}}{n}$=$\frac{{n}^{2}+2n+1}{n}$,
右边=n+1+$\frac{n+1}{n}$=$\frac{{n}^{2}+n+n+1}{n}$=$\frac{{n}^{2}+2n+1}{n}$,
∵左边=右边,
∴(n+1)×$\frac{n+1}{n}$=n+1+$\frac{n+1}{n}$,即猜想成立.
点评 本题考查了规律型中数字的变化类以及有理数的混合运算,解题的关键是:(1)根据等式的变化找出变化规律;(2)利用完全平方公式以及通分将等式左右两边变形为$\frac{{n}^{2}+2n+1}{n}$.


科目:初中数学 来源: 题型:填空题
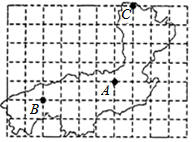 如图是某植物园的平面图,图中A馆所在地用坐标表示为(1,0),B馆所在地用坐标表示为(-3,-1),那么C馆所在地用坐标表示为(2,4).
如图是某植物园的平面图,图中A馆所在地用坐标表示为(1,0),B馆所在地用坐标表示为(-3,-1),那么C馆所在地用坐标表示为(2,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
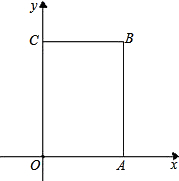 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周).
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
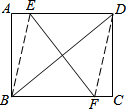 在矩形ABCD中,AB=6cm,BC=8cm,若将矩形对角线BD对折,使B点与D点重合,四边形EBFD是菱形吗?请说明理由,并求这个菱形的边长.
在矩形ABCD中,AB=6cm,BC=8cm,若将矩形对角线BD对折,使B点与D点重合,四边形EBFD是菱形吗?请说明理由,并求这个菱形的边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
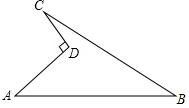 如图是校园内的一块菜地,数学活动小组的同学量得:∠ADC=90°,AD=40m,CD=30m,BC=120m,AB=130m,求这块菜地的面积.
如图是校园内的一块菜地,数学活动小组的同学量得:∠ADC=90°,AD=40m,CD=30m,BC=120m,AB=130m,求这块菜地的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com