
【题目】在△ABC中,AB=AC,点D为射线CB上一个动点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作EF∥BC,交直线AC于点F,连接CE.
(1)如图①,若∠BAC=60°,按边分类:△CEF是 ____________ 三角形;
(2)若∠BAC<60°.
①如图②,当点D在线段CB上移动时,判断△CEF的形状并证明;

②当点D在线段CB的延长线上移动时,△CEF是什么三角形?请在图③中画出相应的图形,写出结论并证明.
【答案】(1)等边;(2)①△BEF为等腰三角形,②△EFB为等腰三角形(3)等腰三角形
【解析】
试题(1)、根据题意推出△AED和△ABC为等边三角形,然后通过求证△EAF≌△DAC,结合平行线的性质,即可推出△EFC为等边三角形;(2)、①根据(1)、的推理依据,即可推出△EFC为等腰三角形;②根据题意画出图形,然后根据平行线的性质,通过求证△EAF≌△DAC,推出等量关系,即可推出△CEF为等腰三角形.
试题解析:(1)、等边;
(2)、①△CEF为等腰三角形,
理由如下:∵AB=AC,AD=AE,∠BAC=∠DAE,∴△AED和△ABC为等腰三角形,
∴∠ACB=∠ABC,∠EAD=∠CAE,∴△EAC≌△BAD,∴∠ABC=∠ACE,∵EF∥BC,
∴∠EFC=∠ACB,∵在△EFB中,∠EFC=∠ACE, ∴△EFB为等腰三角形,
②AB=AC,点D为射线BC上一个动点(不与B、C重合),以AD为一边向AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作BC的平行线,交直线AB于点F,连接BE.
∵△BEF为等腰三角形,∵AB=AC,AD=AE,∠BAC=∠DAE,
∴△AED和△ABC为等腰三角形, ∴∠ACB=∠ABC,∠EAB=∠DAC,
∴△EAF≌△DAC, ∴∠EBA=∠ACD, ∴∠EBF=∠ACB,
∵EF∥BC, ∴∠AFE=∠ABC, ∵∠ABC=∠ACB, ∴∠AFE=∠ACB,
∵在△EFB中,∠EBF=∠AFE, ∴△EFB为等腰三角形.
(3)、等腰三角形.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】为积极创建全国文明城市,某市对某路口的行人交通违章情况进行了 ![]() 天的调查,将所得数据绘制成如下统计图(图2不完整):
天的调查,将所得数据绘制成如下统计图(图2不完整):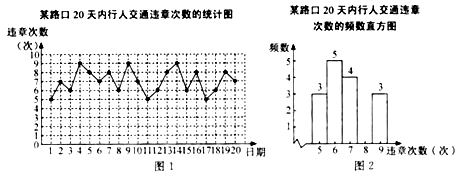
请根据所给信息,解答下列问题:
(1)第 ![]() 天,这一路口的行人交通违章次数是多少次?这
天,这一路口的行人交通违章次数是多少次?这 ![]() 天中,行人交通违章
天中,行人交通违章 ![]() 次的有多少天?
次的有多少天?
(2)请把图2中的频数直方图补充完整;
(3)通过宣传教育后,行人的交通违章次数明显减少.经对这一路口的再次调查发现,平均每天的行人交通违章次数比第一次调查时减少了 ![]() 次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章?
次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 ![]() :
: ![]() 与直线
与直线 ![]() :
: ![]() 相交于点P(1,b)
相交于点P(1,b)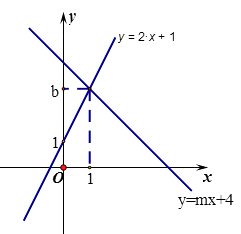
(1)求b,m的值
(2)垂直于x轴的直线 ![]() 与直线
与直线 ![]() ,
, ![]() 分别相交于C,D,若线段CD长为2,求a的值
分别相交于C,D,若线段CD长为2,求a的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】判断下列各式从等号左边到右边的变形,哪些是整式乘法,哪些是因式分解.
(1)a2-9b2=(a+3b)(a-3b);
(2)3y(x+2y)=3xy+6y2;
(3)(3a-1)2=9a2-6a+1;
(4)4y2+12y+9=(2y+3)2;
(5)x2+x=x2(1+![]() );
);
(6)x2-y2+4y-4=(x-y)(x+y)+4(y-1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 平面内,没有公共点的两条线段平行
B. 平面内,没有公共点的两条射线平行
C. 没有公共点的两条直线互相平行
D. 互相平行的两条直线没有公共点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y= ![]() (x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )
(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( ) 
A.减小
B.增大
C.先减小后增大
D.先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳OB的长为3m,静止时,踏板到地面距离BD的长为0.6m(踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为hm,成人的“安全高度”为2m(计算结果精确到0.1m) 
(1)当摆绳OA与OB成45°夹角时,恰为儿童的安全高度,则h=m
(2)某成人在玩秋千时,摆绳OC与OB的最大夹角为55°,问此人是否安全?(参考数据: ![]() ≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一次函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求m的值;
(2)画出此函数的图象;
(3)平移此函数的图象,使得它与两坐标轴所围成的图形的面积为4,请直接写出此时图象所对应的函数关系式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com