练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．在-2、1、-$\sqrt{5}$、0这四个数中，最小的实数是（　　）
    A．-2B．1C．-$\sqrt{5}$D．0

    分析 正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小，据此判断即可．

    解答 解：根据实数比较大小的方法，可得
    1＞0＞-2＞-$\sqrt{5}$，
    ∴在-2、1、-$\sqrt{5}$、0这四个数中，最小的实数是-$\sqrt{5}$．
    故选：C．

    点评 此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正实数＞0＞负实数，两个负实数绝对值大的反而小．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    18．某居民小区开展节约用水活动，3月份各户用水量比2月份有所下降，不同节水量的户数统计如下表所示：
    节水量（立方米）1 23
    　户数2012060
    那么3月份平均每户节水量是（　　）
    A．1.9立方米B．2.2立方米C．33.33立方米D．66.67立方米

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

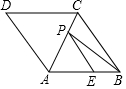    19．如图，菱形ABCD的边长为5，对角线AC=2$\sqrt{5}$，点E在边AB上，BE=2，点P是AC上的一个动点，则PB+PE的最小值为2$\sqrt{13}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

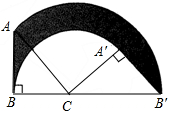    16．如图，等腰Rt△ABC中，∠B=90°，AB=1，将Rt△ABC绕点C按顺时针方向旋转，得到Rt△A′B′C，且B、C、B′三点共线，则边AB扫过的面积（图中阴影部分）是$\frac{3}{8}π$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．计算：（-$\frac{1}{3}$）-2+|$\sqrt{3}$-2|-2tan60°+$\sqrt{27}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算：（-2）0-（-$\frac{1}{3}$）2×3+（-1）3÷$\frac{3}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

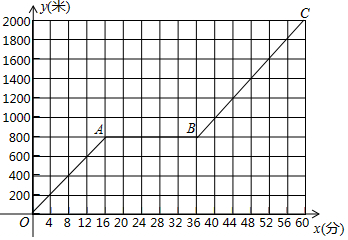    20．小明家到公园的路程为2000米，小明爸爸和小明先后从家出发步行去公园．爸爸先出发一直匀速前行，小明在爸爸走出200米后出发，途中他在休闲广场观棋停留一段时间．小明所走路程y（米）与步行时间x（分）的函数图象如图所所示．
    （1）求直线BC所对应的函数表达式．
    （2）在小明出发后的第20分钟，爸爸与小明第二次相遇，请在图中画出爸爸所走的路程y（米）与小明的步行时间x（分）的函数图象．
    （3）在速度都不变的情况下，小明希望比爸爸早8分钟到达公园，请直接写出小明怎样调整在休闲广场的观棋时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知：如图，抛物线y=ax2+bx+c与x轴交于两个不同的点A（-4，0），B（1，0），与y轴正半轴交于点C，tan∠CAB=$\frac{1}{2}$．
    （1）求抛物线的解析式并验证点Q（-1，3）是否在抛物线上；
    （2）点M是线段AC上一动点（不与A，C重合），过点M作x轴的垂线，垂足为H，交抛物线于点N，试判断当MN为最大值时，以MN为直径的圆与y轴的位置关系并说明理由；
    （3）已知过点B的直线y=x-1交抛物线于另一点E，问：在x轴上是否存在点P，使以点P，A，Q为顶点的三角形与△AEB相似？若存在，请求出所有符合要求的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．某市中学组织学生到距离学校6km的神舟科技馆去参观，学生李伟因事故耽误没能乘上学校的专车，于是准备在学校门口改乘出租车去神舟科技馆，出租车的收费标准如下：
     里程 收费
     2km以内（含2km） 10.0
     2km以上，每增加1km 1.40
    （1）写出出租车行驶的里程数x（x≥2km）与费用y（元）之间的函数关系式；
    （2）李伟同学身上仅有16元钱，乘出租车到科技馆的车费够不够？请说明理由．

    查看答案和解析>>

    同步练习册答案