
【题目】如图,四边形ABCD中,AB∥CD,AB≠CD,AC=DB.
(1)求证:AD=BC;
(2)若E,F,G,H分别是AB,CD,AC,BD的中点,求证:线段EF与线段GH互相平分.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)由平行四边形的性质易得AC=BM=BD,∠BDC=∠M=∠ACD,由全等三角形判定定理及性质得出结论;
(2)连接EH,HF,FG,GE,E,F,G,H分别是AB,CD,AC,BD的中点,易得四边形HFGE为平行四边形,由平行四边形的性质及(1)结论得HFGE为菱形,易得EF与GH互相垂直平分.
证明:(1)过点B作BM∥AC交DC的延长线于点M,如图1,

∵AB∥CD
∴四边形ABMC为平行四边形.
∴AC=BM=BD,∠BDC=∠M=∠ACD.
在△ACD和△BDC中,
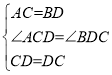 ,
,
∴△ACD≌△BDC(SAS),
∴AD=BC;
(2)连接EH,HF,FG,GE,如图2,
∵E,F,G,H分别是AB,CD,AC,BD的中点,
∴HE∥AD,且HE=![]() AD,FG∥AD,且FG=
AD,FG∥AD,且FG=![]() ,
,
∴四边形HFGE为平行四边形,
由(1)知,AD=BC,
∴HE=EG,
∴HFGE为菱形,
∴EF与GH互相垂直平分.



科目:初中数学 来源: 题型:
【题目】某商品现在售价为每件60元,每星期可卖出300件,市场调查反映:调整价格,每件涨价1元,每星期要少卖出10件;每件降价1元,每星期可多卖出20件.已知商品的进价为每件40元.
(1)设每件降价x元,每星期的销售利润为y元;
① 请写出y与x之间的函数关系式;
② 确定x的值,使利润最大,并求出最大利润;
(2)若涨价x元,则x= 元时,利润y的最大值为 元(直接写出答案,不必写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜有限公司一年四季都有大量新鲜蔬菜销往全国各地,近年来它的蔬菜产值不断增加,2014年蔬菜的产值是640万元,2016年产值达到1000万元.
(1)求2015年、2016年蔬菜产值的平均增长率是多少?
(2)若2017年蔬菜产值继续稳定增长(即年增长率与前两年的年增长率相同),那么请你估计2017年该公司的蔬菜产值达到多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
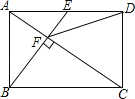
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=![]() S△ABF,其中正确的结论有________个。
S△ABF,其中正确的结论有________个。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于F,OE⊥OB交BC边于点E.
(1)求证:△ABF∽△COE;
(2)当O为AC边中点, ![]() 时,如图2,求
时,如图2,求![]() 的值;
的值;
(3)当O为AC边中点, ![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将举行“数学知识竞赛”活动,班长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:
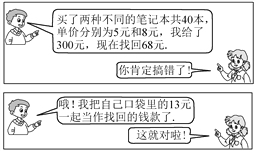
请根据上面的信息,解决问题:
(1)试计算两种笔记本各买了多少本?
(2)请你解释:小明为什么不可能找回68元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将平行四边形 ABCD 沿对角线 BD 折叠,使点 A 落在A′处,若∠1=∠2=50°,则∠A′的度数为( )

A.100°B.105°C.110°D.115°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如图1,将线段AB平移至线段CD,连接AC、BD.
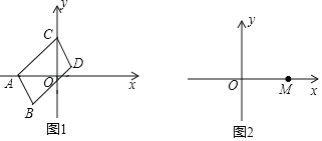
(1)已知A(﹣3,0)、B(﹣2,﹣2),点C在y轴的正半轴上,点D在第一象限内,且三角形ACO的面积是6,求点C、D的坐标;
(2)如图2,在平面直角坐标系中,已知一定点M(1,0),两个动点E(a,2a+1)、F(b,﹣2b+3).
①请你探索是否存在以两个动点E、F为端点的线段EF平行于线段OM且等于线段OM,若存在,求出点E、F两点的坐标;若不存在,请说明理由;
②当点E、F重合时,将该重合点记为点P,另当过点E、F的直线平行于x轴时,是否存在△PEF的面积为2?若存在,求出点E、F两点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com