
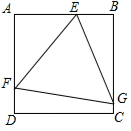
 如图,正方形ABCD的边长为18,正三角形EFG内接于此正方形,且E、F、G分别在边AB、AD、BC上,若AE=12,则BG=10$\sqrt{3}$.
如图,正方形ABCD的边长为18,正三角形EFG内接于此正方形,且E、F、G分别在边AB、AD、BC上,若AE=12,则BG=10$\sqrt{3}$. 分析 如图,作EK⊥FG于K,则K是FG的中点,连接AK,BK,首先利用四点共圆证明△ABK是等边三角形,在Rt△EMK中求出EK,再求出EG,最后在Rt△EBG中利用勾股定理即可解决问题.
解答 解:如图,作EK⊥FG于K,则K是FG的中点,连接AK,BK,
∴∠EKG=∠EBG=∠EKF=∠EAF=90°,
∴E、K、G、B和E、K、F、A分别四点共圆,
∴∠KBE=∠EGK=60°,∠EAK=∠EFK=60°,
∴△ABK是等边三角形,
∴AB=AK=KB=18,
作KM⊥AB,则M为AB的中点,
∴KM=AK•sin60°=9$\sqrt{3}$,
∵AE=12,AM=9,
∴EM=12-9=3,EB=18=12=6,
∴EK=$\sqrt{M{K}^{2}+M{E}^{2}}$=6$\sqrt{7}$,
∴EG=$\frac{EK}{sin60°}$=4$\sqrt{21}$,
在Rt△EGB中,BG=$\sqrt{E{G}^{2}-E{B}^{2}}$=$\sqrt{(4\sqrt{21})^{2}-{6}^{2}}$=10$\sqrt{3}$.
故答案为10$\sqrt{3}$.
点评 本题考查正方形的性质、等边三角形的判定和性质、勾股定理等知识,解题的关键是灵活应用勾股定理解决问题,本题用到四点共圆是个难点,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
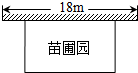 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E.
如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com