
【题目】在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
(1)将△ABC向下平移5个单位长度,画出平移后的A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C.

【答案】(1)作图见解析;点A1的坐标为(4,﹣1);(2)作图见解析;(3)作图见解析.
【解析】试题分析:(1)根据网格结构找出点A、B、C向下平移5个单位的对应点A1、B1、C1的位置,然后顺次连接即可,再根据平面直角坐标系写出点A1的坐标;
(2)根据网格结构找出点A、B、C关于点y轴对称的对应点A2、B2、C2的位置,然后顺次连接即可,再根据平面直角坐标系写出点A2的坐标即可;
(3)根据三角形的面积公式求出△ABC的面积.
试题解析:(1)如图所示,△A1B1C1即为所求作的三角形,点A1的坐标(4,-1);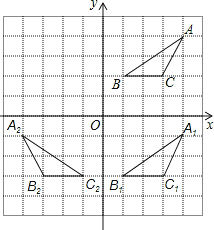
(2)如图所示,△A2B2C2即为所求作的三角形;A2(-4,-1);
(3)S△ABC=![]() ×2×2=2.
×2×2=2.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】平某游泳馆暑期推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费20元;方式二:不购买会员证,每次游泳付费25元.设小明计划今年暑期游泳次数为x(x为正整数).根据题意列表:
游泳次数 | 5 | 8 | 10 | … | x |
方式一的总费用( | 200 | 260 | m | … | |
方式二的总费用( | 125 | 200 | 250 | … |
(1)表格中的m值为 ;
(2)根据题意分别求出两种付费方式中![]() 与自变量x之间的函数关系式并画出图象;
与自变量x之间的函数关系式并画出图象;
(3)请你根据图象,帮助小明设计一种比较省钱的付费方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着出行方式的多样化,某地区打车有三种乘车方式,收费标准如下(假设打车的平均车速为30千米/小时):
网约出租车 | 网约顺风车 | 网约专车 |
3千米以内:12元 | 1.5元/千米 | 2元/千米 |
超过3千米的部分:2.4元/千米 | 0.5元/分钟 | 0.6元/分钟 |
(如:乘坐6千米,耗时12分钟,网约出租车的收费为:12+2.4×(6-3)=19.2(元);网约顺风车的收费为:6×1.5+12×0.5=15(元);网约专车的收费为:6×2+12×0.6=19.2(元))
请据此信息解决如下问题:
(1)王老师乘车从纵棹园去汽车站,全程8千米,如果王老师乘坐网约出租车,需要支付的打车费用为______元;
(2)李校长乘车从纵掉园去生态园,乘坐网约顺风车比乘坐网约出租车节省了2元.求从纵棹园去生态园的路程;
(3)网约专车为了和网约顺风车竞争客户,分别推出了优惠方式:网约顺风车对于乘车路程在5千米以上(含5千米)的客户每次收费立减6元;网约专车打车车费一律七五折优惠.对采用哪一种打车方式更合算提出你的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() 试说明直线AD与BC垂直
试说明直线AD与BC垂直![]() 请在下面的解答过程的空格内填空或在括号内填写理由
请在下面的解答过程的空格内填空或在括号内填写理由![]() .
.
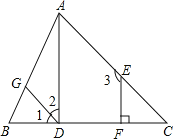
理由:![]() ,
,![]() 已知
已知![]()
![]() ______
______![]() ______,
______,![]() ______
______![]()
![]() ______
______![]() ______
______![]()
又![]() ,
,![]() 已知
已知![]()
![]() ______
______![]() 等量代换
等量代换![]()
![]() ______
______![]() ______,
______,![]() ______
______![]()
![]() ______
______![]()
![]() ,
,![]() 已知
已知![]()
![]() ,
,![]() ,
,
![]() ______
______![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
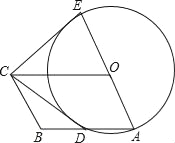
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=4,CD=6,求平行四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,下列条件中,不能使四边形DBCE成为菱形的是( )
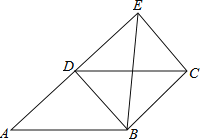
A.AB=BEB.BE⊥DCC.∠ABE=90°D.BE平分∠DBC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知y﹣2与x成正比例,且x=2时,y=﹣6.①求y与x之间的函数关系式;②当y<3时,求x的取值范围.
(2)已知经过点(﹣2,﹣2)的直线l1:y1=mx+n与直线l2:y2=﹣2x+6相交于点M(1,p)
①关于x,y的二元一次方程组![]() 的解为 ;②求直线l1的表达式.
的解为 ;②求直线l1的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
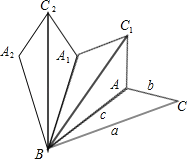
【题目】在△ABC中,∠ABC<20°,三边长分别为a,b,c,将△ABC沿直线BA翻折,得到△ABC1;然后将△ABC1沿直线BC1翻折,得到△A1BC1;再将△A1BC1沿直线A1B翻折,得到△A1BC2;…,若翻折4次后,得到图形A2BCAC1A1C2的周长为a+c+5b,则翻折11次后,所得图形的周长为_____________.(结果用含有a,b,c的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com