
 如图,平行四边形ABCD的对角线AC,BD交于点O,过点B作BP∥AC,过点C作CP∥BD,BP与CP相交于点P.
如图,平行四边形ABCD的对角线AC,BD交于点O,过点B作BP∥AC,过点C作CP∥BD,BP与CP相交于点P.分析 (1)根据两组对边互相平行,即可得出四边形BPCO为平行四边形;
(2)根据菱形的对角线互相垂直,即可得出∠BOC=90°,结合(1)结论,即可得出四边形BPCO为矩形;
(3)根据正方形的性质可得出OB=OC,且OB⊥OC,再根据平行四边形的性质可得出OD=OB,OA=OC,进而得出AC=BD,再由AC⊥BD,即可得出四边形ABCD是正方形.
解答 解:(1)四边形BPCO为平行四边形,理由如下:
∵BP∥AC,CP∥BD,
∴四边形BPCO为平行四边形.
(2)四边形BPCO为矩形,理由如下:
∵四边形ABCD为菱形,
∴AC⊥BD,则∠BOC=90°,
由(1)得四边形BPCO为平行四边形,
∴四边形BPCO为矩形.
(3)四边形ABCD是正方形,理由如下:
∵四边形BPCO是正方形,
∴OB=OC,且OB⊥OC.
又∵四边形ABCD是平行四边形,
∴OD=OB,OA=OC,
∴AC=BD,
又∵AC⊥BD,
∴四边形ABCD是正方形.
点评 本题考查了正方形的判定与性质、平行四边形的判定与性质、菱形的性质以及矩形的判定,解题的关键是:(1)利用两组对比互相平行的四边形为平行四边形得出四边形BPCO为平行四边形;(2)利用有一个直角的平行四边形为矩形得出四边形BPCO为矩形;(3)找出AC=BD且AC⊥BD.本题属于基础题,难度不大,解决该题型题目时,牢记各特殊图形的判定与性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
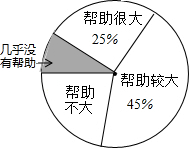 为了解“数学思想作文对学习数学帮助有多大?”研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和表1来表示(图、表都没制作完成).
为了解“数学思想作文对学习数学帮助有多大?”研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和表1来表示(图、表都没制作完成).| 选项 | 帮助很大 | 帮助较大 | 帮助不大 | 几乎没有帮助 |
| 人数 | a | 540 | 270 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,线段AB,C是线段AB上一点,M是AB的中点,N是AC的中点.
如图,线段AB,C是线段AB上一点,M是AB的中点,N是AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com