
 经过点B.
经过点B.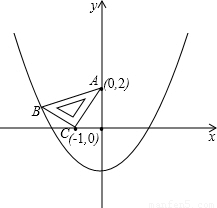
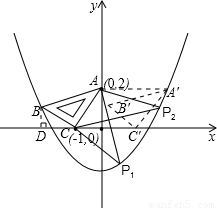 解:(1)过B作BD⊥x轴于D;
解:(1)过B作BD⊥x轴于D; =1,
=1, ;
; x2+
x2+ x-
x- .
. x2+
x2+ x-
x- =2,
=2, ×(
×(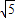 )2+3×2=8.5(平方单位).
)2+3×2=8.5(平方单位). x2+
x2+ x-
x- 于P1,
于P1, x-
x- ;
; x2+
x2+ x-
x- 于P2,易求得直线AF的解析式为y=-
于P2,易求得直线AF的解析式为y=- x+2;
x+2;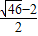 ,
,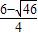 )或(
)或(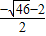 ,
,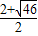 )(不合题意舍去);
)(不合题意舍去);

科目:初中数学 来源: 题型:
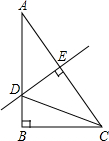 (2013•石峰区模拟)如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,若BD=1,则AC的长是
(2013•石峰区模拟)如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,若BD=1,则AC的长是| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
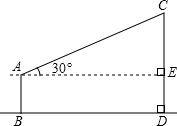 (2013•石峰区模拟)如图所示,小明测量学校旗杆的高度,他在离电线杆CD距离为15米的地方放置一个高1.5米的测角仪(AB),此时,经A处测得旗杆上顶端C处的仰角为30°.请问:这样就能够测出旗杆CD的高度吗?如果能,CD的高是多少米?(结果精确到0.1)
(2013•石峰区模拟)如图所示,小明测量学校旗杆的高度,他在离电线杆CD距离为15米的地方放置一个高1.5米的测角仪(AB),此时,经A处测得旗杆上顶端C处的仰角为30°.请问:这样就能够测出旗杆CD的高度吗?如果能,CD的高是多少米?(结果精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:
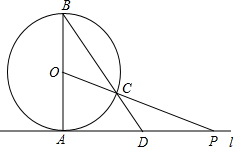 (2013•石峰区模拟)如图,已知直线L与⊙O相切于点A,直径AB=6,点P在L上移动,连结OP交⊙O于点C,连结BC并延长BC交直线l于点D.
(2013•石峰区模拟)如图,已知直线L与⊙O相切于点A,直径AB=6,点P在L上移动,连结OP交⊙O于点C,连结BC并延长BC交直线l于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com