
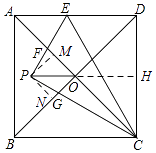
【题目】如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,点E是AD边上一点,连接CE,把△CDE沿CE翻折,得到△CPE,EP交AC于点F,CP交BD于点G,连接PO,若PO∥BC,则四边形OFPG的面积是 . 
【答案】8﹣4 ![]()
【解析】解:如图所示,过P作PM⊥AO于M,作PN⊥BO于N,延长PO交CD于H,
∵PO∥BC,BC⊥CD,
∴PH⊥CD,
又∵△CDO是等腰直角三角形,
∴OH= ![]() CD=2=CH,OH平分∠COD,
CD=2=CH,OH平分∠COD,
由折叠可得,CP=CD=4,
∴Rt△PCH中,PH= ![]() =2
=2 ![]() ,
,
∴PO=PH﹣OH=2 ![]() ﹣2,
﹣2,
∵PO平分∠AOB,PM⊥AO,PN⊥BO,
∴PM=PN,
矩形PMON是正方形,
∴正方形PMON的面积= ![]() OP2=
OP2= ![]() (2
(2 ![]() ﹣2)2=8﹣4
﹣2)2=8﹣4 ![]() ,
,
∵∠FPG=∠MON=90°,
∴∠FPM=∠GPN,
在△PMF和△PNG中,
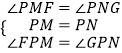 ,
,
∴△PMF≌△PNG(ASA),
∴S△PMF=S△PNG,
∴S四边形OFPG=S正方形PMON,
∴四边形OFPG的面积是8﹣4 ![]() ,
,
所以答案是:8﹣4 ![]() .
.
【考点精析】利用等腰直角三角形和勾股定理的概念对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 ![]() 的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
(1)求以A,B,C,D为顶点的四边形的面积;
(2)在抛物线上是否存在点P,使得△ABP的面积是△ABC的面积的2倍?若存在,求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,将一块等腰直角三角形的直角顶点放在斜边
,将一块等腰直角三角形的直角顶点放在斜边![]() 的中点
的中点![]() 处,将三角板绕点
处,将三角板绕点![]() 旋转,三角板的两直角边分别交射线
旋转,三角板的两直角边分别交射线![]() 、
、![]() 于
于![]() 、
、![]() 两点.如图①、②、③是旋转三角板得到的图形中的3种情况.
两点.如图①、②、③是旋转三角板得到的图形中的3种情况.
(1)观察图①,当三角板绕点![]() 旋转到
旋转到![]() 时,我们发现:
时,我们发现:![]() __________
__________![]() .(选填“
.(选填“![]() ”、“
”、“![]() ”或“
”或“![]() ”)
”)
(2)当三角板绕点![]() 旋转到图②所示位置时,判断(1)题中
旋转到图②所示位置时,判断(1)题中![]() 与
与![]() 之间的大小关系还存在吗?请你结合图②说明理由.
之间的大小关系还存在吗?请你结合图②说明理由.
(3)三角板绕点![]() 旋转,
旋转,![]() 是否能成为等腰三角形?若能,指出所有情况(那写出
是否能成为等腰三角形?若能,指出所有情况(那写出![]() 为等腰三角形时
为等腰三角形时![]() 的长);若不能,请说明理由.
的长);若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)图1中阴影部分面积为______,图2中阴影部分面积为_____,对照两个图形的面积可以验证________公式(填公式名称)请写出这个乘法公式________.
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有![]() 、
、![]() 两种型号的客车共20辆,它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下,共载客720人.
两种型号的客车共20辆,它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下,共载客720人.
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
(1)求![]() 、
、![]() 两种型号的客车各有多少辆?
两种型号的客车各有多少辆?
(2)某中学计划租用![]() 、
、![]() 两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元. 求最多能租用多少辆A型号客车?
两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元. 求最多能租用多少辆A型号客车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1和∠2互为补角,∠A=∠D,求证:∠B=∠C.

请在下面的证明过程的括号内,填写依据.
证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD( )
∵∠1+∠2=180°(已知)
∴∠2+∠CGD=180°(等量代换)
∴AE//FD( )
∴∠AEC=∠D( )
∵∠A=∠D(已知)
∴∠AEC=∠A( )
∴AB//CD( )
∴∠B=∠C( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得到△A′PB.
(1)如图2所示,当PA′⊥BC时,求线段PA的长度.
(2)当∠DPA′=10°时,求∠APB的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com