
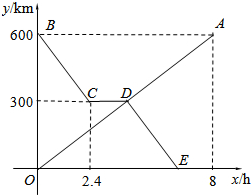
 货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发3h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.
货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发3h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.分析 (1)待定系数求出OA解析式,继而根据点D的纵坐标为300求得其横坐标,即可得答案;
(2)根据休息前2.4小时行驶300km可得行驶后行驶300km也需要2.4h,即可得点E坐标,待定系数法即可求得DE所在直线解析式;
(3)先求出BC所在直线解析式,再根据①轿车休息前与货车相距200km,②轿车休息后与货车相距200km,分别列出方程求解可得.
解答 解:(1)设OA所在直线解析式为y=mx,
将x=8、y=600代入,求得m=75,
∴OA所在直线解析式为y=75x,
令y=300得:75x=300,解得:x=4,
∴点D 坐标为( 4,300 ),其实际意义为:点D是指货车出发4h后,与轿车在距离甲地300 km处相遇.
(2)由图象知,轿车在休息前2.4小时行驶300km,
∴根据题意,行驶后300km需2.4h,
故点E 坐标( 6.4,0 ).
设DE所在直线的函数表达式为y=kx+b,
将点D ( 4,300 ),E ( 6.4,0)代入y=kx+b得:
$\left\{\begin{array}{l}{4k+b=300}\\{6.4k+b=0}\end{array}\right.$,
得 $\left\{\begin{array}{l}{b=800}\\{k=-125}\end{array}\right.$,
∴DE所在直线的函数表达式为y=-125x+800.
(3)设BC段函数解析式为:y=px+q,
将点B(0,600)、C(2.4,300)代入,得:
$\left\{\begin{array}{l}{q=600}\\{2.4p+q=300}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{p=-125}\\{q=600}\end{array}\right.$,
y=-125x+600,
①当轿车休息前与货车相距50km时,有:-125x+600-75x=50或300-75x=50,解得:x=2.75(不合题意舍弃)或x=$\frac{10}{3}$;
②当轿车休息后与货车相距50km时,有:75x-(-125x+800)=50,解得:x=4.25;
故答案为:$\frac{10}{3}$或5.
点评 本题考查了一次函数的应用,待定系数法是求函数解析式的关键,注意分类讨论思想的渗透.


科目:初中数学 来源: 题型:填空题
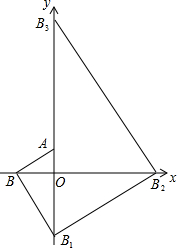 把多块大小不同的30°直角三角板如图所示,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0,1),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2;第四块三角板的斜边B2B3与第三块三角板的斜边B1B2垂直且交y轴于点B3;…按此规律继续下去,则点B2017的坐标为(0,-31009).
把多块大小不同的30°直角三角板如图所示,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0,1),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2;第四块三角板的斜边B2B3与第三块三角板的斜边B1B2垂直且交y轴于点B3;…按此规律继续下去,则点B2017的坐标为(0,-31009).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
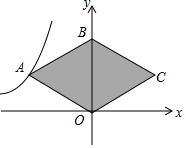 如图,O是坐标原点,菱形OABC的顶点B的坐标为(0,4),反比例函数y=-$\frac{8}{x}$(x<0)的图象经过点A,则菱形OABC的面积为16.
如图,O是坐标原点,菱形OABC的顶点B的坐标为(0,4),反比例函数y=-$\frac{8}{x}$(x<0)的图象经过点A,则菱形OABC的面积为16.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
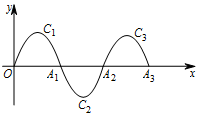 如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,若点P(2017,m)在第1009段抛物线C1009上,则m的值为( )
如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,若点P(2017,m)在第1009段抛物线C1009上,则m的值为( )| A. | -1 | B. | 0 | C. | 1 | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
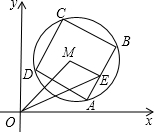 如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.
如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com