
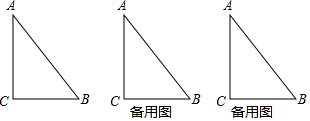
分析 (1)由t=2可知点P在线段AC上,利用勾股定理可求得BP的长,则可求得△ABP的周长;
(2)过C作CP⊥AB于点P,可求得CP的长,则可求得AP的长,当点P在线段AC上时,可知满足条件,当CP⊥AB时也满足条件,从而可求得t的取值范围;
(3)△BCP为等腰三角形时,分三种情况进行讨论:①CP=CB;②BC=BP;③PB=PC.
解答 解:(1)∵∠C=90°,AC=8,BC=6,
∴有勾股定理得AB=10,动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2个单位
∴出发2秒后,则CP=4,那么AP=4,
∵∠C=90°,
∴由勾股定理得PB=2$\sqrt{13}$,
∴△ABP的周长为:AP+PB+AB=4+10+2$\sqrt{13}$=14+2$\sqrt{13}$;
(2)如图,作CP⊥AB于P.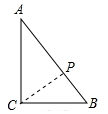
∵$\frac{1}{2}$•AB•CP=$\frac{1}{2}$•AC•BC,
∴CP=$\frac{AC•BC}{AB}$=$\frac{6×8}{10}$=$\frac{24}{5}$,
∴AP=$\sqrt{A{C}^{2}-P{C}^{2}}$=$\frac{32}{5}$,
∴当∠CPB=90°时,t=(8+$\frac{32}{5}$)÷2=$\frac{36}{5}$,
当点P在线段AC上时,∠PCB=90°,此时△PCB是直角三角形,
∴当0<t≤4或t=$\frac{36}{5}$s时,△PCB是直角三角形.
(3)△BCP为等腰三角形时,分三种情况:
①如果CP=CB,那么点P在AC上,CP=6cm,此时t=6÷2=3(秒);
如果CP=CB,那么点P在AB上,CP=6cm,此时t=5.4(秒)
(点P还可以在AB上,此时,作AB边上的高CD,利用等面积法求得CD=4.8,再利用勾股定理求得DP=3.6,所以BP=7.2,AP=2.8,所以t=(8+2.8)÷2=5.4(秒))
②如果BC=BP,那么点P在AB上,BP=6cm,CA+AP=8+10-6=12(cm),此时t=12÷2=6(秒);
③如果PB=PC,那么点P在BC的垂直平分线与AB的交点处,即在AB的中点,此时CA+AP=8+5=13(cm),
t=13÷2=6.5(秒);
综上可知,当t=3秒或5.4秒或6秒或6.5秒时,△BCP为等腰三角形.
点评 本题考查了勾股定理,等腰三角形的判定,三角形的周长与面积,三角形的中线等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
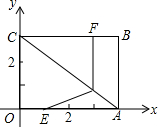 如图在平面直角坐标系中,四边形OABC是矩形,OA=4cm,OC=3cm,动点E、F分别从O、B同时出发,以1cm/s的速度运动,其中,点E眼OA向终点A点运动,点F沿BC向终点C点运动,过点F作FP⊥BC,交AC于点P,连接EP,设运动时间为xs.
如图在平面直角坐标系中,四边形OABC是矩形,OA=4cm,OC=3cm,动点E、F分别从O、B同时出发,以1cm/s的速度运动,其中,点E眼OA向终点A点运动,点F沿BC向终点C点运动,过点F作FP⊥BC,交AC于点P,连接EP,设运动时间为xs.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.05×1010吨 | B. | 1.05×109吨 | C. | 10.5×108吨 | D. | 1.105×1010吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b2=a2-c2 | B. | ∠C=∠A-∠B | C. | ∠A:∠B:∠C=3:4:5 | D. | $a:b:c=3:4:\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 摸球的次数n | 1000 | 1500 | 2000 | 5000 | 8000 | 10000 |
| 摸到白球的次数m | 582 | 960 | 1161 | 2954 | 4842 | 6010 |
| 摸到白球的频率 | 0.582 | 0.64 | 0.5805 | 0.5908 | 0.6053 | 0.601 |
| A. | 20 | B. | 25 | C. | 30 | D. | 35 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com