
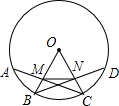
 如图,在⊙O中,$\widehat{AB}=\widehat{BC}=\widehat{CD}$,半径OB,OC分别交弦AC,BD于点M,N,求证:∠OMN=∠ONM.
如图,在⊙O中,$\widehat{AB}=\widehat{BC}=\widehat{CD}$,半径OB,OC分别交弦AC,BD于点M,N,求证:∠OMN=∠ONM. 分析 由$\widehat{AB}=\widehat{BC}=\widehat{CD}$,可得∠AOB=∠BOC=∠DOC,进而根据OA=OB=OC得出OB⊥AC,OC⊥BD,由垂径定理得出AM=MC=$\frac{1}{2}$AC=BN=DN=$\frac{1}{2}$BD,然后根据HL证得RT△AOM≌RT△DON,即可证得OM=ON,根据等边对等角即可证得结论.
解答 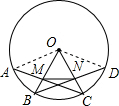 证明:连接OA、OD,
证明:连接OA、OD,
∵$\widehat{AB}=\widehat{BC}=\widehat{CD}$,
∴∠AOB=∠BOC=∠DOC,
∵OA=OB=OC,
∴OB⊥AC,OC⊥BD,
∴AM=MC=$\frac{1}{2}$AC,BN=DN=$\frac{1}{2}$BD,
∵$\widehat{AB}=\widehat{BC}=\widehat{CD}$,
∴$\widehat{ABC}$=$\widehat{BCD}$,
∴AC=BD,
∴AM=DN,
在RT△AOM和RT△DON中,
$\left\{\begin{array}{l}{OA=OD}\\{AM=DN}\end{array}\right.$
∴RT△AOM≌RT△DON(HL),
∴OM=ON,
∴:∠OMN=∠ONM.
点评 考查的是圆心角、弧、弦的关系、垂径定理以及三角形全等的判定和性质,熟练掌握性质定理是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
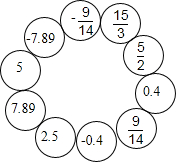 某天,黄新同学遇到了一个这样的涂色游戏:如图,把每一对互为相反数所在的色框涂上你喜欢的不同颜色;绝对值为5的数所在的色框涂上蓝色;到数轴原点距离为2.5的数所在的色框涂上黑色,感兴趣的你赶快试试吧!
某天,黄新同学遇到了一个这样的涂色游戏:如图,把每一对互为相反数所在的色框涂上你喜欢的不同颜色;绝对值为5的数所在的色框涂上蓝色;到数轴原点距离为2.5的数所在的色框涂上黑色,感兴趣的你赶快试试吧!查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com