
【题目】已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC. 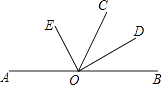
(1)求∠EOD的度数;
(2)若∠AOE=50°,求∠BOC的度数.
【答案】
(1)解:∵OE、OD分别平分∠AOC、∠BOC,
∴∠EOC= ![]() ∠AOC,∠COD=
∠AOC,∠COD= ![]() ∠BOC,
∠BOC,
∴∠EOD=∠EOC+∠COD= ![]() ∠AOC+
∠AOC+ ![]() ∠BOC=
∠BOC= ![]() ∠AOB,
∠AOB,
又∵A、O、B三点在同一直线上,
∴∠AOB=180°,
∴∠EOD= ![]() ∠AOB=90°
∠AOB=90°
(2)解:∵OE平分∠AOC,∠AOE=50°,
∴∠AOC=2∠AOE=100°,
∴∠BOC=180°﹣∠AOC=80°
【解析】(1)由于OE、OD分别平分∠AOC、∠BOC,所以∠EOC= ![]() ∠AOC,∠COD=
∠AOC,∠COD= ![]() ∠BOC,进而得出∠EOD=∠EOC+∠COD=
∠BOC,进而得出∠EOD=∠EOC+∠COD= ![]() ∠AOB=90°;(2)由OE平分∠AOC,∠AOE=50°,得出∠AOC=2∠AOE=100°,再根据邻补角定义得出∠BOC=180°﹣∠AOC=80°.
∠AOB=90°;(2)由OE平分∠AOC,∠AOE=50°,得出∠AOC=2∠AOE=100°,再根据邻补角定义得出∠BOC=180°﹣∠AOC=80°.
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线).


科目:初中数学 来源: 题型:
【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n= ![]() .
.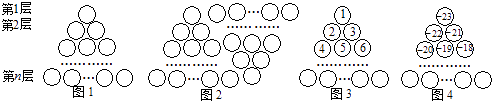
如果图中的圆圈共有11层,请问:自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层中间这个圆圈中的数是;自上往下,在每个圆圈中按图4的方式填上一串连续的整数
﹣23,﹣22,﹣21,﹣20,…,则所有圆圈中各数之和为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
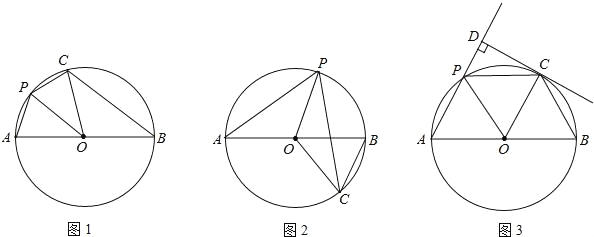
【题目】已知,AB是⊙O的直径,点P在弧AB上(不含点A、B),把△AOP沿OP对折,点A的对应点C恰好落在⊙O上.
(1)当P、C都在AB上方时(如图1),判断PO与BC的位置关系(只回答结果);
(2)当P在AB上方而C在AB下方时(如图2),(1)中结论还成立吗?证明你的结论;
(3)当P、C都在AB上方时(如图3),过C点作CD⊥直线AP于D,且CD是⊙O的切线,证明:AB=4PD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,垂足为点A,AB=12,AC=6,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过 秒时,△DEB与△BCA全等.
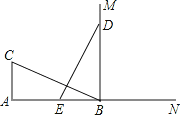
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:
如图1,△ABC中,∠A=90°,∠B=30°,点D,E分别在AB,BC上,且∠CDE=90°.当BE=2AD时,图1中是否存在与CD相等的线段?若存在,请找出并加以证明,若不存在,说明理由.
小明通过探究发现,过点E作AB的垂线EF,垂足为F,能得到一对全等三角形(如图2),从而将解决问题.
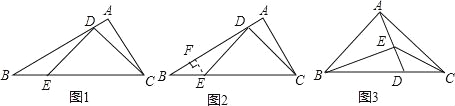
请回答:
(1)小明发现的与CD相等的线段是 .
(2)证明小明发现的结论;
参考小明思考问题的方法,解决下面的问题:
(3)如图3,△ABC中,AB=AC,∠BAC=90°,点D在BC上,BD=2DC,点E在AD上,且∠BEC=135°,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com