
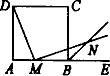
如图,已知点M是正方形ABCD的边AB上的中点,MN⊥DM,与∠ABC外角的平分线交于N.求证:MD=MN.
|
分析 MD和MN所在的两个三角形明显不全等,要想用全等三角形证明两条线段相等,就要添辅助线.∠DMN=90°,不难发现∠MDA=∠NMB.要想两个三角形全等,至少要有一条边对应相等,即P为AD的中点,则有DP=MB,在△PDM和△BMN中,只要再有一个角相等即可证明它们全等,由已知条件可推出∠DPM=∠MBN=135°.问题至此解决. 证明 取AD的中点P,连结PM,△PDM和△BMN中,∵∠DMN=90°∴∠NMB+∠DMA=90°.又∠MDA+∠DMA=90°.∴∠NMB=∠MDA.即∠NMB=∠MDP.又∵M为AB的中点,P为AD的中点,∴MB=DP.又∵AP=AM,△APM为等腰直角三角形,∠APM=45°,∠MPD=135°,BN为∠ABC外角平分线,∠NBE=45°,∠NBM=135°.∴∠DPM=∠NBM.△PDM≌△BMN,∴DM=MN. |


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
 ,
,| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | x |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知正方形ABCD的边长为4,将正方形置于平面直角坐标系xOy中,使AB在x轴的负半轴上,A点的坐标是(-1,0).
如图,已知正方形ABCD的边长为4,将正方形置于平面直角坐标系xOy中,使AB在x轴的负半轴上,A点的坐标是(-1,0).| 12 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知B(0,4),点A在第一象限,且AB⊥y轴,∠A=30°.
如图,已知B(0,4),点A在第一象限,且AB⊥y轴,∠A=30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A、B、C是数轴上三点,O为原点.点C对应的数为6,BC=4.AB=12.
如图,已知点A、B、C是数轴上三点,O为原点.点C对应的数为6,BC=4.AB=12. CQ,设运动时间为t(t>0).
CQ,设运动时间为t(t>0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com