
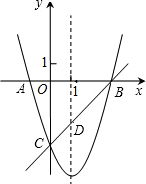
 如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.分析 (1)利用对称轴公式即可得出b的值,再利用抛物线与y轴交于点C(0,-3),求出抛物线解析式即可;
(2)分两种情形①过C作AB的平行线,交抛物线于M1,此时△M1AB与△ABC的面积相等.点C关于x轴的对称点C′(0,3),过C′作x轴的平行线,与抛物线交于点M2,M3,此时M2,M3也满足条件,
(3)①首先求出直线BC的解析式,进而得出D点坐标,进而得出EG和DG的长进而求出即可;根据相似三角形的相似条件画出图形即可解决问题.
解答 解:(1)∵抛物线的对称轴为直线x=1,
∴-$\frac{b}{2a}$=-$\frac{b}{2}$=1,
∴b=-2
∵抛物线与y轴交于点C(0,-3),
∴c=-3,
∴抛物线的函数表达式为:y=x2-2x-3;
(2)如图1中,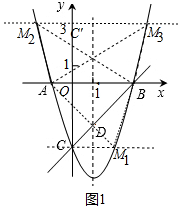
∵抛物线与x轴交于A、B两点,
当y=0时,x2-2x-3=0.
∴x1=-1,x2=3.
∵A点在B点左侧,
∴A(-1,0),B(3,0)
①过C作AB的平行线,交抛物线于M1,
此时△M1AB与△ABC的面积相等.
根据对称性可知点M1坐标为(2,-3),
②点C关于x轴的对称点C′(0,3),过C′作x轴的平行线,与抛物线交于点M2,M3,
此时M2,M3也满足条件,
对于抛物线y=x2-2x-3,
当y=3时,x2-2x-3=3,解得x=1$±\sqrt{7}$,
∴M2(1-$\sqrt{7}$,3),M2(1+$\sqrt{7}$,3).
综上所述满足条件的点M坐标为(2,-3)或(1-$\sqrt{7}$,3)或(1+$\sqrt{7}$,3).
(3)如图2中,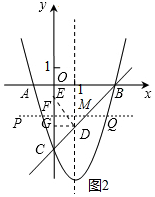
①∵AB=4,PQ=$\frac{3}{4}$AB,
∴PQ=3
∵PQ⊥y轴
∴PQ∥x轴,
则由抛物线的对称性可得PM=$\frac{3}{2}$,
∵对称轴是直线x=1,
∴P到y轴的距离是 $\frac{1}{2}$,
∴点P的横坐标为-$\frac{1}{2}$,
∴P(-$\frac{1}{2}$,-$\frac{7}{4}$)
∴F(0,-$\frac{7}{4}$),
∴FC=3-OF=3-$\frac{7}{4}$=$\frac{5}{4}$∵PQ垂直平分CE于点F,
∴CE=2FC=$\frac{5}{2}$,
∵点D在直线BC上,
∴当x=1时,y=-2,则D(1,-2),
过点D作DG⊥CE于点G,
∴DG=1,CG=1,
∴GE=CE-CG=$\frac{5}{2}$-1=$\frac{3}{2}$.
在Rt△EGD中,tan∠CED=$\frac{GD}{EG}$=$\frac{2}{3}$.
②如图3中,当△CEG与△AOC相似时,点E的坐标为(0,$\frac{1}{3}$) 或(0,0)或(0,-$\frac{8}{3}$)或(0,-$\frac{10}{3}$)或(0,-6)或(0,-$\frac{19}{3}$).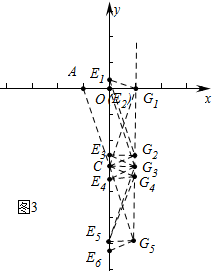
点评 本题主要考查了二次函数的综合题型以及直角三角形的性质和待定系数法求一次函数解析式等知识,利用直角三角形的性质得出a的值是解题关键,学会分类讨论的思想解决问题,注意最后一个问题答案比较多,考虑问题要全面,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
 如图,在∠MON的两边上取A,B两点,连AB,分别以OA,AB为边,在∠MON内作等边△OAD和等边△ABC,连CD,求证:OB=DC.
如图,在∠MON的两边上取A,B两点,连AB,分别以OA,AB为边,在∠MON内作等边△OAD和等边△ABC,连CD,求证:OB=DC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图(1),将一个边长为2的正方形分割成四个完全相同的直角三角形,然后把这4个直角三角形无缝隙不重叠的拼成如图(2)所示的大正方形,若图(2)中的小正方形边长是1,则图(2)中大正方形的边长是( )
如图(1),将一个边长为2的正方形分割成四个完全相同的直角三角形,然后把这4个直角三角形无缝隙不重叠的拼成如图(2)所示的大正方形,若图(2)中的小正方形边长是1,则图(2)中大正方形的边长是( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{a}$ | B. | $\sqrt{-10}$ | C. | $\sqrt{a+1}$ | D. | $\sqrt{{a}^{2}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 将l1向上平移6个单位长度 | B. | 将l1向下平移6个单位长度 | ||
| C. | 将l1向左平移6个单位长度 | D. | 将l1向右平移6个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com