
 上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).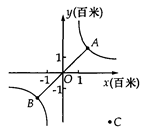
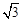 ,-2
,-2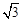 )
)| 分析: | (1)A、B两点直线y=x上和双曲线y=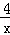 ,列方程组可求A、B两点坐标,在依题意判断△ABC为等边三角形,OA=2 ,列方程组可求A、B两点坐标,在依题意判断△ABC为等边三角形,OA=2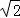 ,则OC= ,则OC=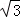 OA=2 OA=2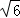 ,过C点作x轴的垂线CE,垂足为E,利用OC在第四象限的角平分线上求OE,CE,确定C点坐标; ,过C点作x轴的垂线CE,垂足为E,利用OC在第四象限的角平分线上求OE,CE,确定C点坐标;(2)分别求出AC、OC的长,分别表示教练船与A、B两船的速度与时间,比较时间的大小即可. |
| | 解:(1)CE⊥x轴于E,解方程组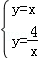 得 得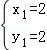 , ,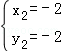 ∴A(2,2),B(﹣2,﹣2), 在等边△ABC中可求OA=2 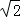 , ,则OC= 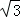 OA=2 OA=2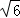 , ,在Rt△OCE中,OE=CE=OC?sin45°=2 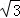 , ,∴C(2 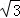 ,﹣2 ,﹣2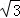 ); );(2)作AD⊥x轴于D,连AC、BC和OC, ∵A(2,2), ∴∠AOD=45°,AO=2 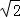 , ,∵C在O的东南45°方向上, ∴∠AOC=45°+45°=90°, ∵AO=BO,∴AC=BC, 又∵∠BAC=60°, ∴△ABC为正三角形, ∴AC=BC=AB=2AO=4 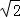 , ,∴OC= 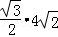 =2 =2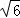 , ,由条件设教练船的速度为3m,A、B两船的速度都为4m, 则教练船所用时间为 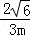 ,A、B两船所用时间均为 ,A、B两船所用时间均为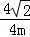 = =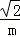 , ,∵ 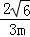 = =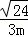 , ,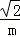 = =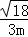 , ,∴ 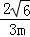 > >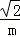 ; ;∴教练船没有最先赶到. 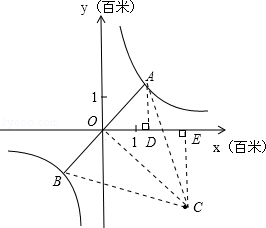 |
| 点评: | 本题考查了直角坐标系中点的求法,根据点的坐标求两点之间距离的方法.解答本题时同学们要读懂题意,就不易出错. |


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源:不详 题型:解答题
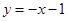 与反比例函数
与反比例函数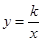 的图象都过点A(
的图象都过点A(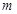 ,1)。
,1)。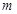 的值,并求反比例函数的解析式;
的值,并求反比例函数的解析式;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的
的
| A.2 | B.4 | C. | D. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
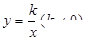 ,在每个象限内y随着x的增大而增大,点P(a-1, 2)在这个反比例函数上,a的值可以是( )
,在每个象限内y随着x的增大而增大,点P(a-1, 2)在这个反比例函数上,a的值可以是( )| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与x轴、
与x轴、 轴分别交于点C、
轴分别交于点C、 ,与反比例函数
,与反比例函数 (k≠0)相交于A、D两点,其中BD=5,BO=2,
(k≠0)相交于A、D两点,其中BD=5,BO=2, .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com