
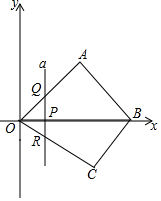
 如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上,∠OAB=90°且OA=AB,OB=6,OC=5.
如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上,∠OAB=90°且OA=AB,OB=6,OC=5.分析 (1)根据等腰直角三角形的性质即可解决问题;
(2)首先求出直线OA、OB、OC、BC的解析式.①求出P、Q的坐标即可解决问题;
②分三种情形分别求解即可解决问题;
③利用②中的函数,利用配方法求出最值即可;
解答 解:(1)由题意△ OAB是等腰直角三角形,
OAB是等腰直角三角形,
∵OB=6,
∴A(3,3),B(6,0).
(2)∵A(3,3),B(6,0),
∴直线OA的解析式为y=x,直线AB的解析式y=-x+6,
∵t=4时,直线a恰好过点C,OC=5,
∴C(4,-3),
∴直线OC的解析式为y=-$\frac{3}{4}$x,直线BC的解析式为y=$\frac{3}{2}$x-9,
①当0<t<3时,Q(t,t),R(t,-$\frac{3}{4}$t),
∴m=t+$\frac{3}{4}$t=$\frac{7}{4}$t.
②当0<t<3时,S=$\frac{1}{2}$PE•QR=$\frac{1}{2}$•(6-2t)•$\frac{7}{4}$t=-$\frac{7}{4}$t2+$\frac{21}{4}$t,
当3<t<4时,S=$\frac{1}{2}$•PE•QR=$\frac{1}{2}$(2t-6)•(-t+6+$\frac{3}{4}$t)=-$\frac{1}{4}$t2+$\frac{27}{4}t$-18,
当4≤t<6时,S=$\frac{1}{2}$•PE•QR=$\frac{1}{2}$(2t-6)(-t+6-$\frac{3}{2}$t+9)=-$\frac{5}{2}$t2+$\frac{45}{2}$t-45.
③当0<t<3时,∵S=-$\frac{7}{4}$t2+$\frac{21}{4}$t=-$\frac{7}{4}$(x-$\frac{3}{2}$)2+$\frac{63}{16}$,∴t=$\frac{3}{2}$时,S的最大值为$\frac{63}{16}$.
当3<t≤4时,∵S=-$\frac{1}{4}$t2+$\frac{27}{4}t$-18=-$\frac{1}{4}$(t-$\frac{27}{2}$)2+$\frac{1}{4}$×$\frac{2{7}^{2}}{4}$-18,∴t=4时,S的值最大,最大值为5.
当4≤t<6时,S=-$\frac{5}{2}$t2+$\frac{45}{2}$t-45=-$\frac{5}{2}$(t-$\frac{9}{2}$)2+$\frac{35}{8}$,∴t=$\frac{9}{2}$时,S的最大值为$\frac{35}{8}$,
综上所述,t=4时,S的值最大,最大值为5,
故答案为5.
点评 本题考查四边形综合题、一次函数的应用、二次函数的应用、等腰直角三角形的性质等知识,解题的关键是学会构建一次函数或二次函数解决实际问题,属于中考压轴题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,C为⊙O外一点,且∠CAB=90°,BD是⊙O的弦,BD∥CO.
如图,AB为⊙O的直径,C为⊙O外一点,且∠CAB=90°,BD是⊙O的弦,BD∥CO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 种树、种草每亩每年补粮补钱情况表 | ||
| 种树 | 种草 | |
| 补粮 | 150千克 | 100千克 |
| 补钱 | 200元 | 150元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
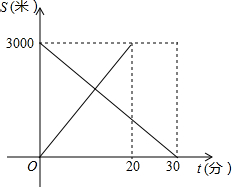 甲从A地出发,匀速步行到B地,同时,乙从B地出发,匀速步行到A地,甲乙两人与A地的距离S(米)与出发时间t(分钟)的关系如图:
甲从A地出发,匀速步行到B地,同时,乙从B地出发,匀速步行到A地,甲乙两人与A地的距离S(米)与出发时间t(分钟)的关系如图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com