
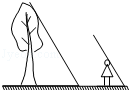
 某数学兴趣小组利用太阳光测量一棵树的高度(如图),在同一时刻,测得树的影长为4.8米,小明的影长为1.2米,已知小明的身高为1.5米,则树高为6米.
某数学兴趣小组利用太阳光测量一棵树的高度(如图),在同一时刻,测得树的影长为4.8米,小明的影长为1.2米,已知小明的身高为1.5米,则树高为6米.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 向西走了15千米 | B. | 向东走了15千米 | C. | 向西走了5千米 | D. | 向东走了5千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
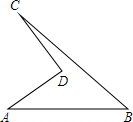 实验中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,若每平方米草皮需要300元,学校需要投入多少资金买草皮?
实验中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,若每平方米草皮需要300元,学校需要投入多少资金买草皮?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com