
分析 由关于x的一元二次方程mx2-6x+1=0有两个不相等的实数根,根据一元二次方程的定义和根的判别式的意义可得m≠0且△>0,即62-4•m•1>0,两个不等式的公共解即为m的取值范围.
解答 解:∵关于x的方程mx2-6x+1=0有两个不相等的实数根,
∴m≠0且△>0,即62-4•m•1>0,
解得m<9,
∴m的取值范围为m<9且m≠0.
故答案为:m<9且m≠0.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△<0,方程有两个相等的实数根;当△=0,方程没有实数根;也考查了一元二次方程的定义.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
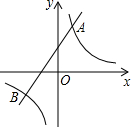 已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2)
已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
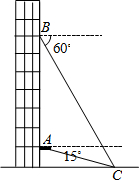 从一幢建筑大楼的两个观察点A,B观察地面的花坛(点C),测得俯角分别为15°和60°,如图,直线AB与地面垂直,AB=50米,试求出点B到点C的距离.(结果保留根号)
从一幢建筑大楼的两个观察点A,B观察地面的花坛(点C),测得俯角分别为15°和60°,如图,直线AB与地面垂直,AB=50米,试求出点B到点C的距离.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
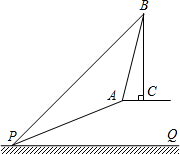 如图,已知斜坡AP的坡度为i=1:$\sqrt{3}$,坡长AP为20m,与坡顶A处在同-水平面上有-座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角α且tanα=3.求:
如图,已知斜坡AP的坡度为i=1:$\sqrt{3}$,坡长AP为20m,与坡顶A处在同-水平面上有-座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角α且tanα=3.求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
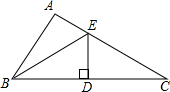 如图,已知△ABC中,AB<AC,BC边上的垂直平分平分线DE交BC于点D,交AC于点E,若AC=10cm,△ABE的周长为18cm,求AB的长.
如图,已知△ABC中,AB<AC,BC边上的垂直平分平分线DE交BC于点D,交AC于点E,若AC=10cm,△ABE的周长为18cm,求AB的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com