
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,对角线
,对角线![]() ,
,![]() 相交于点
相交于点![]() .点
.点![]() 是线段
是线段![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合),连接
重合),连接![]() ,以
,以![]() 为边在
为边在![]() 的右侧作
的右侧作![]() ,且
,且![]() ,
,![]() .
.
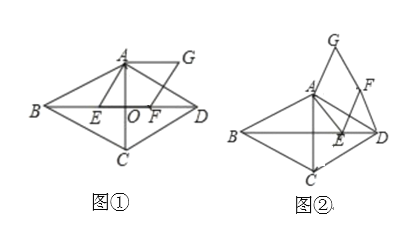
(1)如图①,若点![]() 落在线段
落在线段![]() 上,则线段
上,则线段![]() 与线段
与线段![]() 的数量关系是______;
的数量关系是______;
(2)如图②,若点![]() 不在线段
不在线段![]() 上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
【答案】(1)AE=BE;(2)成立,理由见解析
【解析】
(1)先根据题意判断![]() 是菱形,再利用菱形的性质得出∠ABO=∠ADO=30°,AC⊥BD,即可求出∠FAD=30°即可得出结论;
是菱形,再利用菱形的性质得出∠ABO=∠ADO=30°,AC⊥BD,即可求出∠FAD=30°即可得出结论;
(2)先判断出△ACD和△AEF是等边三角形,进而得出∠CAE=∠DAF,即可判断出△ACE≌△ADF,即可得出结论.
(1)如图,连接AF,
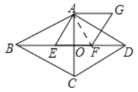
∵![]() ,且
,且![]() ,
,
∴四边形ABCD是菱形,
∴AC⊥BD,∠ABO=![]() ∠ABC=30°,
∠ABC=30°,
∴∠OAE=∠OAF=30°,
∴∠DAF=30°=∠ADO,
∴AF=FD,
∵AF=EF,
∴EF=FD;
∵∠AEF=60°,
∴∠BAE=30°=∠ABO,
∴AE=BE.
(2)成立,如图,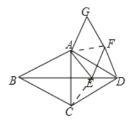
连接CE,AF,
∵四边形ABCD是菱形,四边形AEFG是菱形,
∴AD=CD,AE=EF,BD垂直平分AC,∠ABC=∠ADC=60°,
∴∠ADC=∠AEF=60°,
∴△ACD和△AEF是等边三角形,
∴AC=AD,AE=AF=EF,∠CAD=∠EAF=60°,
∴∠CAE=∠DAF,
在△ACE和△ADF中, 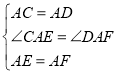 ,
,
△ACE≌△ADF(SAS),
∴EC=DF,
∵BD垂直平分AC,
∴EC=AE,
∴DF=AE=EF


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图, AB∥CD, AC∥BD, AD与BC交于O, AE⊥BC于E, DF⊥BC于F, 那么图中全等的三角形有 ( )
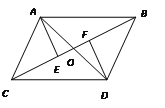
A.5对B.6对C.7对D.8对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市为了美化环境,计划在如图所示的三角形空地上种植草皮,已知这种草皮每平方米售价为![]() 元,则购买这种草皮至少需要______元.(用含
元,则购买这种草皮至少需要______元.(用含![]() 的式子表示)
的式子表示)
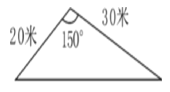
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,3),B(5,1),C(1,3),结合所给的平面直角坐标系,解答下列问题: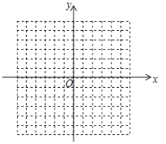
(1)请在如图坐标系中画出△ABC;
(2)画出△ABC关于x轴对称的△A′B′C′,并写出△A′B′C′各顶点坐标;
(3)在x轴上找一点P,使PA+PB的值最小。请画出点P,并求出点P坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=8,求△OEC的面积.
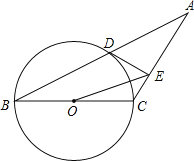
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOC和∠DOB都是直角.
(1)如图1,∠DOC=![]() ,则∠AOB= 度;
,则∠AOB= 度;
(2)在图1中,如果∠DOC≠![]() ,找出图中相等的锐角,并说明理由;
,找出图中相等的锐角,并说明理由;
(3)在图2中,利用三角板画一个与∠FOE相等的角.

查看答案和解析>>
科目:初中数学 来源: 题型:
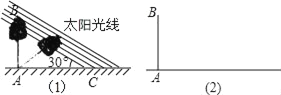
【题目】某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com