
 已知点A是双曲线y=$\frac{2}{x}$在第一象限上的动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
已知点A是双曲线y=$\frac{2}{x}$在第一象限上的动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )| A. | y=-$\frac{2}{x}$(x<0) | B. | y=-$\frac{4}{x}$(x<0) | C. | y=-$\frac{6}{x}$(x<0) | D. | y=-$\frac{8}{x}$(x<0) |
分析 设点A的坐标为(a,$\frac{2}{a}$),连接OC,则OC⊥AB,表示出OC,过点C作CD⊥x轴于点D,设出点C坐标,在Rt△OCD中,利用勾股定理可得出x2的值,继而得出y与x的函数关系式.
解答  解:过点C作CD⊥x轴于点D,连接OC,
解:过点C作CD⊥x轴于点D,连接OC,
设A(a,$\frac{2}{a}$),
∵点A与点B关于原点对称,
∴OA=OB,
则B(-a,-$\frac{2}{a}$)
∵△ABC为等边三角形,
∴AB⊥OC,OC=$\sqrt{3}$AO,
∵AO=$\sqrt{{a}^{2}+(\frac{2}{a})^{2}}$,
∴CO=$\sqrt{3}$×$\sqrt{{a}^{2}+(\frac{2}{a})^{2}}$=$\sqrt{3{a}^{2}+\frac{12}{{a}^{2}}}$,
∵∠BOD+∠COD=∠COD+∠OCD=90°,
∴∠BOD=∠OCD,
设点C的坐标为(x,y),则tan∠BOD=tan∠OCD,即$\frac{\frac{2}{a}}{a}$=$\frac{-x}{y}$,
解得:y=-$\frac{{a}^{2}}{2}$x,
在Rt△COD中,CD2+OD2=OC2,即y2+x2=3a2+$\frac{12}{{a}^{2}}$,
将y=-$\frac{{a}^{2}}{2}$x代入,得($\frac{{a}^{4}+4}{4}$)x2=3($\frac{{a}^{4}+4}{{a}^{2}}$),
解得:x2=$\frac{12}{{a}^{2}}$,
故x=$\frac{2\sqrt{3}}{a}$,y=-$\sqrt{3}$a,
则xy=-6,
故可得:y=-$\frac{6}{x}$(x>0).
故选C.
点评 本题考查了反比例函数的综合题,涉及了解直角三角形、等边三角形的性质及勾股定理的知识.注意准确作出辅助线是解此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+1)•(2+x) | B. | ($\frac{1}{2}$a+b)•(b-$\frac{1}{2}$a) | C. | (-a+b)•(a-2b) | D. | (-x-$\frac{1}{2}$y)•($\frac{1}{2}$x+y) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
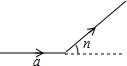 小明同学在社团活动中给发明的机器人设置程序:(a,n).机器人执行步骤是:向正前方走am后向左转n°,再依次执行相同程序,直至回到原点.现输入a=6,n=40,那么机器人回到原点共走了54m.
小明同学在社团活动中给发明的机器人设置程序:(a,n).机器人执行步骤是:向正前方走am后向左转n°,再依次执行相同程序,直至回到原点.现输入a=6,n=40,那么机器人回到原点共走了54m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 产品 | 每件产品的产量 | 每件产品用工时数 |
| 甲 | 45万元 | 150 |
| 乙 | 75万元 | 190 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com